( Notation: Symbols normally in sub-script are preceded by a comma.
Powers, normally in super-script, are preceded by a a single quotation mark,
tho x-squared, for instance, is written the normal way, x². )
Links to sections:
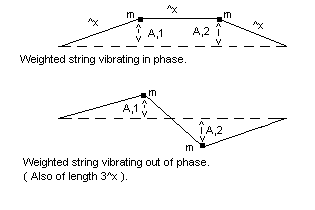
An example of a coupled oscillator is two weights oscillating on the same
stretched piece of string. If they oscillate with each other, they will shape
the string into an arch when they go up together, and into a dip or bowl's
outline, when they go down together. Their oscillations are said to be in
phase.
The weights are exactly out of phase, when they are moving in exactly the
opposite directions. So, when one weight had jumped up to its furthest, the
other weight has jumped down its furthest. If the two objects are the same
weight, they have gone equal distances in the opposite direction. ( That
assumes gravity doesnt exert an important downward pull, in this case. )
The out-of-phase motion of the weights gives the string a zig-zag shape of one wave-length. The in-phase motion, over the same length of string, forms half a wave-length. Therefore, the in-phase half wave-length is twice the length of a half wave-length for the out-of-phase string motion.
The more weights there are to coupled oscillators, the more their oscillations approximate to smooth wave motions. So, coupled oscillators were originally studied as an aid to understanding the properties of waves. In particular, they approximate to the wave equation, as a partial differential equation, when the weights are assumed to be continuous along a length of string, in effect given a certain mass density, forming smooth ( not zig-zag or angular ) waves.
The two previous web pages considered ordinary differential wave equations ( damped or undamped ) where the displacement, from equilibrium, of a weighted spring, or of a tense string, was the dependent variable on one independent variable, the time. But oscillations can take place in space, as well as time, for instance, if the weighted spring acted on the surface of a liquid, making waves.
Likewise, visible waves are formed along a length of tensed string. In a partial differential equation, the string displacement is a function of at least two independent variables, time and space in one dimension, if not two or three dimensions, as physical waves can be linear, planar or spherical.
There are two basic kinds of waves, longitudinal waves and transverse
waves. If you fasten a piece of string to a post and hold the other end, you
can make longitudinal waves with a quick back and forward move of the hand.
Transverse or perpendicular waves are made by an up and down jerk of the hand.
The strength and direction of the waves depends on the energy and direction of
the motion you impart to them.
Likewise, a hammer tap, to the end of a metal bar, along its length, sets up
longitudinal vibrations. Whereas, a tap downward, near one end, sets up
transverse vibrations in the bar.
In simple terms, the mathematical form of the partial differential equation of wave motion, for instance in the metal rod, is much the same. The classical wave equation of the vibrating string is for transverse motion.
In the two previous web pages, difference equations were considered as more or less approximate substitutes of algebra for the calculus of differential equations. The coupled oscillator serves as a physical model for calculating the difference equation's approximation to a differential equation, because the coupled oscillator's angular wave forms are a physical approximation to smooth wave motion.
In fact, the equation of motion, for the middle of three masses on a
vibrating string, found as a difference equation, is also equal to the
differential equation ( for small displacements of the string ).
See graph:
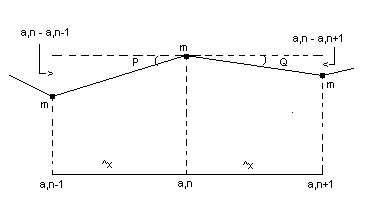 The middle mass, or nth mass, with the highest
displacement from the string's equilibrium, is pulled down on both sides by
the string tension, T.
The middle mass, or nth mass, with the highest
displacement from the string's equilibrium, is pulled down on both sides by
the string tension, T.
That is force, from the left, T sin P = ( a,n - a,n-1 )/ ^x,
and force, from the right, T sin Q = ( a,n - a,n+1 )/ ^x.
By Newton's laws of motion, the joint force of the string tension is equal and opposite to the force, which equals the mass times acceleration, responsible for the displacement, a,n, of the middle weight:
m.d²a,n/dt² = - T( sin P + sin Q )
Therefore, d²a,n/dt² = ( a,n-1 - 2a,n + a,n+1 )T/m.^x.
The right hand side of the equation relates to second order difference equations ( as in web page on the Fibonacci series ). And ( as relates to the previous page on circular function and the ordinary wave equation ) the displacement, a,n can be considered simple harmonic, in time, t, with a frquency of oscillation, w, about its rest position or equilibrium.
That is to say a,n = A,n exp(iwt), where A,n is the maximum displacement.
Exactly the same applies to the displacements of the other two weights, whose displacements, a,n-1 and a,n+1 have their own maximum displacements, A,n-1 and A,n+1, respectively.
The second derivative of a,n can now be equated to its second derivative in exponential form ( as a circular function ) and the three weights' displacements replaced by their maximum displacements:
d²a,n/dt² = - w²A,n.exp(iwt)
= ( A,n-1 - 2A,n + A,n+1 )exp(iwt)T/m.^x.
This reduces to the standard form:
- A,n-1 + ( 2 - ^x.w²m/T )A,n - A,n+1 = 0.
This difference equation of motion for n masses is solved with the equation repeated with substitutions of n = 1, 2, 3, etc up to the number of masses on the string. This calculation is only simple for a few masses.
The following figure is of a string with two masses.

Two masses on the string require the standard form to be solved for n = 1 and n = 2.
To simplify matters further, the tension, T, mass, m, and distance, ^x, between the weights on the string, are all set at one unit.
Substituting n = 1 into the standard form:
( 2 - w² )A,1 - A,2 = 0.
Substituting n = 2 into the standard form:
- A,1 + ( 2 - w² ) A,2 = 0.
A,n-1 in the former substitution equation and A,n+1, in the latter equation both are zero, because they represent the zero-amplitude fixed ends of the string, next to one or other of the two weights. ( A,0 = A,3 = 0. )
By the method of solving simultaneous equations, substitute, say, the value of A,1 in the second equation, into the first equation, so:
( 2 - w² )²A,2 - A,2 = 0.
A,2 can be eliminated and the equation factorised:
( 2 - w² - 1 )( 2 - w² + 1 ) = 0.
Hence, w² is either 1 or 3. The two values for w are the slow and the fast frequencies of oscillation. In the former case, the weights are loosely coupled in phase. In the latter case, the two weights are tightly coupled out of phase. ( See above figure. )
The coupled weights have been considered in terms of their maximum displacements A,1 and A,2. But equations of motion can also be given in terms of the two weights' variable displacements: call them X and Y, respectively. A sketch of the procedure follows.
As with the second derivative for a,n, ( where T, m and ^x, are set at one ) there can be equations for the second derivatives of X and Y:
d²X/dt² = - 2X + Y.
d²Y/dt² = X - 2Y.
These are the equations of motion for the displacements of the two weights.
But equally and oppositely, they are the equations, given opposite signs, of
the forces pulling back the stretched string from those displacements.
It turns out that these equations between string displacements and forces are
the key to a simple expression of their relationship, thru a transformation of
co-ordinates from terms of X and Y to another co-ordinate system, namely of
eigen-vectors ( as discussed in the two previous web pages ).
The reason for this requires some back-ground explanation. Different physical systems may have the same mathematical form, so that their terms are analgous, tho they may not appear alike. The systems are assumed to be closed, with no significant loss of energy thru friction. They both obey conservation of energy, which consists of potential energy and kinetic energy.
When a vibrating string reaches its maximum displacement, all its energy is potential energy. Reaching its furthest extent, its kinetic energy or energy of motion ceases a moment, until it starts to move back in the opposite direction. The string's kinetic energy increases to a maximum at its equilibrium position, when it has no potential energy. Passing this mid-position, it starts to lose kinetic energy again, as the string's displacement increases in the other direction.
Motion on a landscape offers a simple picture, to compare with more complicated-looking systems. On a roller-coaster, potential energy is greatest on the crests, which the vehicle has slowed almost to a stop in reaching. Kinetic energy is greatest in the dip, when maximum acceleration has been reached, and before gravity gradually slows down the charge up the next slope.
Consider a simple system like an oscillating weight on a spring. Potential
energy is given by kx²/2, where k might be the elastic constant of a spring.
Kinetic energy is mv²/2, where m is for mass and v for velocity or rate of
change of x.
The coupled oscillator might also be considered as a spring, instead of a
string, with two inter-mediate masses.
Given that the behaviors of conserved energy systems is determined by their
potential energy and their kinetic energy, these systems can move in step. It
depends if their respective energy constants k and m are the same.
The potential energy of the coupled oscillator, two weights on a stretched
string, is found to be:
X² - XY + Y².
This is determined by finding out how much the string is stretched by the
weights. Knowing the original length of the string ( previously treated as
three unit lengths marked off by the two weights' positions ) the stretched
lengths are found by Pythagoras' theorem and by making use of the fact that
for small k,  ( 1 + k ) ~ 1 + k/2.
( 1 + k ) ~ 1 + k/2.
( The kinetic energy of the coupled system is: m((dX/dt)²)² + (dY/dt)²)/2. )
The motion of a weight on a spring is mathematically analgous to the motion of a ball in a bowl. Likewise, the motion of two weights on a string is analgous to a ball's motion in an oval bowl, a bit like a boat. This can be shown by drawing the graph of the coupled system's potential energy, using the X and Y axes of the two weights' displacements, with the potential energy as a third dimension of height.
For any given constant level of potential energy, an oval contour is mapped
onto the graph, forming a series of nested ovals depending on the 'height' of
the potential energy. This is just like the geographical map of a valley,
whose contours would show a perfectly oval hollow.
But the length and the breadth of this hollow or boat are not in line with the
X and Y co-ordinates. Instead, they are at forty-five degrees to them. To
measure the length and breadth of the potential energy hollow directly would
require new axes, call them U and V, at forty-five degrees to the old
axes.
Assuming no loss of energy thru friction, the motion of a ball, from top to top, the length of the hollow, is analgous, in mathematical form, to the in-phase oscillation of the coupled system. This is along the U-axis, at Y = X. The ball rolling from breadth to breadth of the hollow is analgous to the out-of-phase oscillation. This is along the V-axis, where Y = - X. It corresponds to the equal and opposite displacements of the two weights on the string.
These two oscillations ( shown in the above figure ) correspond to the
fundamental and first harmonic in music. Musicians, able to hear both notes at
once, gave mathematicians the idea of adding such basic solutions to get more
complicated solutions.
In terms of a ball rolling down from the rim of the hollow, this means
considering the more complicated motions when the ball rolls other than from a
long end or a broad end. The nearer the ball starts from the long end, the
shallower will be the path of its evolution; the nearer the ball's start from
the broad side, the steeper its roll.
To visualise how this addition of simple solutions can reproduce all possible
motions of the ball in the hollow, one may imagine the ball's motion mimicked
by the spot where two wires cross at right angles. These wires' motions are
governed by their respective attachments to a long spring oscillating at a
lower frequency than a shorter spring. The springs, parallel to the U and V
axes, mimick respectively the long shallow slope and the narrow steep slope of
the hollow.
Indeed, this is a mechanical model of the parallelogram law of vector
addition.
So, it turns out that these new axes are the so-called eigen-vectors or 'proper' vectors, in which to formulate the motion of the system.
Returning to the end of the section on the two-weighted string, the eigen-vectors show an especially simple relation between displacements and forces.
The equations for the displacements, X and Y, of the two weights, are now expressed in terms of the equal and opposite forces, labelled X* and Y*, pulling them back towards the string's equilibrium position:
X* = 2X - Y.
Y* = - X + 2Y.
X and Y, as rectilinear co-ordinates, are, by convention, drawn on a graph pointing to the east and north, respectively. The eigen-vectors V and U are the co-ordinates to the north-west and the north-east, respectively. As, such the ordinate line U is positive with respect to both the X and Y axes. An X,Y co-ordinate position, like 1,1, which is on the U ordinate, can show what happens to the displacement-force equation, in terms of that eigen-vector:
When X* = 2.1 - 1 = 1, and Y* = -1 + 2.1 = 1, the co-ordinates remain unchanged. As discussed on the two previous web pages, the 'eigen-value', of eigen-vector, U, is one.
The situation differs for eigen-vector V, because its position is represented by X,Y co-ordinates, -1,1. Substituting these: X* = -2 - 1 = -3. Y* = - -1 + 2 = 3. In terms of the V axis, the transformation of displacement into force stretches the V axis three times. In other words, the eigen-value of V is three.
The equations of motion, in terms of U and V, are found by substituting X = U + V and Y = U - V into the equations of motion for X and Y. These come out at d²U/dt² = - U and d²V/dt² = - 3V, again showing the simple relation between the opposing forces of string displacing mass and string elasticity, when in terms of the eigenvectors U and V. The solutions of U and V are the usual form for the simple harmonic oscillator:
U = A cos t + B sin t.
V = C cos t 3 + D sin t
3 + D sin t 3.
3.
Where A, B, C, D are constants.
Thus, an under-lying simplicity to the dynamics of the coupled oscillator system is shown up by finding the proper co-ordinates.
The first section of this page mentioned that the coupled oscillator was like a mechanical model of a finite difference equation. This is a discrete version of a differential equation. The masses at periodic intervals on the string are imagined to get smaller and closer until they merge into a continuously dense string, whose vibrations cease to be angular, or zig-zag from the separate action of the weights, but become a continuously smooth wave form.
The equation of motion of the nth mass was given as:
d²a,n/dt² = ( a,n-1 - 2a,n + a,n+1 )T/m.^x.
For the masses to merge into a continuous heavy string, the distances between them must approach zero, or, ^x --> 0.
The bracketed terms relate to a second order finite difference. As shown on the Fibonacci series page, that means they involve a difference between two differences, or a change in a change. So, the equation can be re-written:
d²a,n/dt² = ( ( a,n+1 - a,n )/^x - ( a,n - a,n-1 )/^x )T/m
= ( (^a/^x),n+1 - (^a/^x),n )T/m,
where the ^ sign is meant to serve as a delta sign, used in finite difference equations as the equivalent term to the d for differentiation.
Indeed, ( da/dx ),x+dx - ( da/dx ),x = ( d²a/dx² )dx.
The conditional terms after the commas ( usually denoted as sub-scripts ) need not be considered as ^x --> 0. Therefore:
d²a/dt² = ( d²a/dx² )dx.T/m.
This is the wave equation as a partial differential equation, where the
wave displacement, a, is at position, x, on the string, and at time, t.
The constant, mass per unit length, m/^x, is called the linear density, p. And
T/p = v², where v, in this case, is the phase velocity, or the velocity of the
wave, defined as a 'phase of oscillation'.
Richard Lung.
References:
W W Sawyer: A Path To Modern Mathematics. ( 1966. )
H J Pain: The Physics Of Vibrations And Waves. ( 1980 )
Marcelo Alonso and Edward J Finn: Fundamentals Of University Physics. (
1967 )
( Example 18.5 shows the relation between ordinary and partial differential
wave equations for the longitudinal waves in a spring. )
A later edition has Paul Davies as general editor and is just called:
Physics.