Part One: The Michelson-Morley Experiment and the Lorentz
transformations.
Home page.
Links to sections:
Comments.
Introduction.
The Michelson-Morley Experiment.
The Michelson-Morley calculation (using inappropriate
average).
The Lorentz transformations.
Comments
John Gribbin, in one of his many books on popular science, once derided
special relativity as "ancient history." So great was the growth of natural
science, in the twentieth century compared to the rest of history, a theory
from the beginning of that century must seem out-moded. But he still had to
deal with it, under whatever caption. It is still a starting point of modern
physics.
This treatment of special relativity is not by a professional scientist. It
is just an explanation by a reader of books on popular science. These, quite
rightly, go into the wierd and wonderful consequences of the theory, to inspire
the imaginations of new-comers. This account is more concerned with what are
the (quite simple) formulas behind these consequences. So, no claim is made,
here, to be either inspirational or authoritative. Nor did I pick up any
natural science as a social science student, tho I was particularly interested
in scientific method.
Thousands of books have been written about relativity. Often, a good idea is
given of the mathematics of special relativity. This can be done without going
much, if at all, beyond high school standard. The following account does not
attempt to go beyond fairly basic algebra. (As if I could.)
The math of general relativity is much too advanced for me. And I dont know
of any good popular account of it. Roger Penrose, in The Emperor's New Mind,
gives a thumb-nail sketch of the math involved. He also prefaces Six Not So
Easy Pieces, by Richard Feynman, which gives the best conceptual explanation of
General Relativity, that Ive come across. The "pieces" are, in fact, taken from
his under-graduate text-book on physics. Don't let that put you off. Feynman
approach gives much insight.
If you are a beginner in the subject, it would be better to read first several
introductory works, to fully appreciate Feynmans account of both special and
general relativity. I am glad I didnt come across Six Not So Easy Pieces early
in my reading. And, in fact, my following explanation of special relativity is
not influenced by that book.
To top.
The three related topics to be treated here are the Michelson-Morley
experiment, the Lorentz transformations, and Minkowski Interval. These topics
give precise information, about special relativity, in terms of simple algebra
and geometry.
When I say simple, I mean simple by professional standards. I don't mean that
the math was simple for me to teach myself -- far from it. But I hope my
efforts, such as they are, will give others an easier time of it than I had.
The name "the theory of special relativity" (as well as of "general
relativity") comes from Albert Einstein. As far as special relativity was
concerned, he gave the physical meaning of what was going on, in such as the
Lorentz transformations.
Minkowski was Einsteins former teacher, who supplied a neater mathematical
form to the equations. At first, Einstein didnt see the point of the new
formalism. But it was to become a point of departure for his general theory.
As for the Michelson-Morley experiment, Einstein said he had heard of it,
when he wrote his famous 1905 paper on special relativity. It was reputed that
he hadnt. Anyway, this experiment is a land-mark to the origin of modern
physics.
To top.
Clerk-Maxwell equations showed that electro-magnetic waves moved at the
speed of light, suggesting that light is an electro-magnetic wave. A wave
normally waves some material medium it moves thru. To talk of a water
wave without water wouldnt seem to make much sense. So, a light wave was held
to manifest the matter of which the universe is made, the so-called universal
"ether." This ether was a supposed "ocean" of material reality thru which light
waves traveled.
(I dont know whether light itself couldnt be considered the medium of light
waves, as water is of water waves. In Feynman quantum theory, light is all over
the place or "oceanic," on the sub-atomic scale. But this is not to the point
of the history of the "ether" as a hypothesis in physics.)
Michelson and Morley set out to detect the ether with an experiment. Given
that the ether was the all-pervading medium of the universe, its
characteristics, such as velocity, could not be related to any thing else. The
ether would have its own definitive or absolute velocity, like the velocity of
a stream relative to ones position on the bank. (Absolute velocity seems a
self-contradiction. It can only be conceived in relative terms and therefore is
not absolute. This is perhaps a cue for Einstein principle of relativity.)
In the Michelson-Morley experiment, ones position on the "bank" is akin to
ones position on Earth relative to a universal ether "stream."
The experiment can be explained by continuing the analogy with the stream. One
could take two return journeys of equal distance on the stream. Taking into
account the velocity of the stream, simple geometry shows which journey would
take the longest and which would take the shortest time.
The return journey, which would be most slowed by stream velocity, is the
one going directly up and down stream. Going down stream (like having a
tail-wind) would be the fastest way for a boat to travel. But having to make a
return trip (like facing a head-wind) would so out-weigh that advantage, that,
on average, the combined up-stream and down-stream trip would be the
slowest.
The quickest return journey, over an equal distance, is the one taken
across-stream and back. Actually, this wouldn't follow a path at right angles
to the banks, because the velocity of the stream is pulling the boat some way
down-stream, while the crossing is being made. And the boat goes adrift by an
equal amount, on the way back to the bank that one embarked from. So, one would
land back some way down the bank, from ones embarkation point.
In the Michelson-Morley experiment, a beam of light stands in for the boat.
This beam is split to do the two different "boat" journeys described. Mirrors
effect the split light beams return journeys.
One light beam was expected to return slightly more slowly than the other, as a
result of a difference in "ether drag" upon the two beams. This is analgous to
the boat going up and down stream taking longer than the boat going across
stream and back.
Of course, no physicist knew the direction of the supposed ether "wind" (to
change the analogy from water to air). But this experiment, with the light beam
split at right angles to itself and reflected, was repeated in all directions,
and at all times in the Earths annual orbit. So, the ether wind direction and
velocity could presumably be infered from the experiment, in that series, which
showed the maximum and minimum delays of a split beam subject to ether drag,
analgous to wind drag.
In fact, the Michelson-Morley experiment showed always the same result: a
null result. The split beams of light always returned with their waves still in
step. An interferometer would have measured interference effects, if they
hadnt. Therefore, the split light waves took the same time to make their two
return journeys, traveling the same distance, without their different
directions causing a more powerful ether drag on one beam than the other. The
speed of light remained constant.
(Eventually, Einstein special theory of relativity would assume there is no
ether and that the speed of light is constant. By this, physicists mean
constant in a vacuum, disregarding that light is slightly slowed in transparent
media, like air and water.)
To top.
This section gives the historic and currently accepted calculation. I showed
elsewhere that if you substitute the geometric mean for the arithmetic mean, to
average the mirror reflected light beam journeys, the correct prediction is
achieved for the result of the famous Michelson-Morley experiement.
The Michelson and Morley calculation, for the experimental result they
expected, is essentially nothing more than simple arithmetic, involving the
fact that light velocity, c, equals distance, d, traveled, divided by the time,
t, taken.
Two different times were predicted, the shortest time, t, for a beam of
light, split to pass athwart the ether stream, and the longest time, which can
be designated t', for the rest of a beam, aligned to the ether stream.
But experiment showed that the times, t and t', were the same. Therefore, to
make the calculation agree with experiment, a factor had to be written into the
calculation, to show t and t' as equal. This factor, would, in effect, contract
the longest time, t', so it equalled the shortest time, t. Hence, its name, the
Fitzgerald-Lorentz contraction factor, after the two physicists, who
independently suggested it.
Eventually, Einstein would dispense with the assumption of ether absolute
velocity and an absolute space and absolute time, presupposed since Newton.
Einstein would explain this contraction factor, in terms of observers, in
different situations or frames of reference, measuring distinct times,
distances and velocities. Different observers could relate their
spatio-temporal measurements, basically thru the so-called contraction factor.
But no one observers frame of reference could be considered absolute, or prior,
to any-one elses. Observations were all relative to each other and no
one was absolute. Hence, the theory of relativity.
How, at first, did Michelson and Morley work out the times, t and t'? The
longest time, t', is the return journey, up and down the ether stream. In other
words, the Earth, at a certain point in its orbit, is supposed to be traveling
in line with the stream of universal ethereal matter. Thereby, the
experimenters light beam is also in line with the ether stream (besides being
split off at right angles to measure the shortest delayed time, t, of light
travel across the ether stream).
Going with the ether stream, the velocity of light, usually given the letter
c, for ("celerity" but I prefer) "constant" velocity, should have a tail-wind
or tail-stream of ether velocity added to it. The ether velocity is given by
earth velocity, just as the velocity of a stream can be measured by the speed
one is running beside its bank to make the stream appear to be standing still.
This ether velocity may be given the letter, u.
The velocity of light with an ether tail-stream was calculated as its own
velocity, c, combined with the ether velocity, u. That is (c+u). Therefore, the
time light takes to travel a distance, d, down-stream was given as the length
divided by the combined velocity, or, d/(c+u).
When the light is reflected, thought of as a boat now going up-stream, it
would be slowed down by the speed of an ether "head-wind," to be subtracted
from the light speed: the light beam speed up-stream was calculated at (c-u).
The up-stream time taken is the slower one of d/(c-u).
Therefore, the combined time, t', for light to travel up and down an ether
"stream" would be
d/(c+u) plus d/(c-u). This works out as 2dc/(c-u)(c+u), or,
2dc/(c²-u²).
For working out the cross-ways return journey, over a comparable distance,
d, of the light beam with respect to the ether stream, please refer to diagram,
below. The light source, S, is the point where the "boat," as light-beam, sets
off across the stream, reflected back by a mirror, M, analgous to a far
"bank."
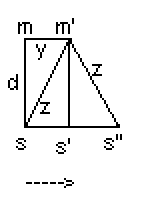 |
Diagram of the Michelson-Morley calculation.
The arrow shows the earths direction, here also defining an "ether
stream," reckoned to cause light the greatest delay, in traveling up
and down stream. The least delay is caused that part of the light beam
that splits across stream. But it is still subject to ether drift
downstream, both to and from M'.
|
But, by the time the light, from source, S, has reached mirror, M, the
mirror has moved to position, M', in the diagram. This is like down-stream
drift on a boat crossing. The same is true for the journey back. So, when the
light-beam reaches M', it has completed half the journey in half the time, t/2.
This is because crossing the ether stream affects journeys, both ways, equally.
There is no element of a head wind one way or a tail wind, the other way.
By the time, the light beam has reached the mirror, at M', the light source,
S, has also traveled half way, S', to its rendezvous, S", with the reflected
light-beam it emitted.
On the diagram, the light beam travels at speed, c, from S to M', given as
distance, z. Meanwhile, the mirror has traveled from M to M', given as
distance, y, down the ether stream, at a speed equated (as explained above) to
earth velocity, u. The two times of travel are equal, actually time t/2, as
mentioned already. Therefore, t/2 equals both distance, z, divided by velocity,
c, and distance, y, divided by velocity, u.
Or, t/2 = z/c = y/u. The distance, z, can be found in terms of Pythagoras
theorem. Namely, z² = y² + d². Therefore, z² = (zu/c)² + d².
And: z²{1 - (u/c)²} = d².
So: z² = d².c²/ (c²-u²).
(c²-u²).
Therefore: z = d{c²/ (c²-u²)}^1/2
(c²-u²)}^1/2
The journey from S to M' is similar to the return from M' to S", also of
distance, z. Therefore, the total distance traveled by a crossing light-speed
"boat" is twice z, or,
2d{c²/ (c²-u²)}^1/2
(c²-u²)}^1/2
Dividing this distance, both ways across, by the light-beam cross-stream
velocity, c, gives its total crossing time, t, as 2d/(c²-u²)^1/2.
This was how Michelson and Morley calculated the two times, t' and t, as a
predicted out-come of maximal and minimal ether drag, respectively.
The fame of their experiment rested on the fact that it showed the two times to
be equal. The two times could only be made equal, in theory as well as
practise, by introducing a factor, F (the so-called Fitzgerald-Lorentz
contraction factor) so that the shorter time, t, equals the longer time, t',
multiplied by the contraction factor.
The contraction factor, F, equals t/t' = {2d/ (c²-u²)^1/2}×{(c²-u²)/2dc}
(c²-u²)^1/2}×{(c²-u²)/2dc}
=  {(c²-u²)^1/2}/c =
{(c²-u²)^1/2}/c =  {1-(u²/c²)}^1/2.
{1-(u²/c²)}^1/2.
To top.
Prof. H A Lorentz showed that Maxwell electrodynamic equations still held,
whether or not subject to a prevailing ether "stream" or "ether wind." But the
co-ordinate systems or frames of reference, of two observers would differ
according as to the extent their measurements were affected by the ether
wind.
Supposing, for the sake of argument, the measurements taken in a laboratory
on earth were not subject to the ether wind. The measurements there are given
by time, t, distance, x, (as well as two other dimensions of space that dont
essentially affect the argument). Lorentz showed that a laboratory elsewhere,
say on a rocket, could still discover Maxwells equations. But the measurements
in the rocket would be in a different frame of reference, with different time,
say, t', different distance, x' (and its two other spatial dimensions).
Consequently, velocities would measure differently: x' = u't', instead of x =
ut.
However, these different co-ordinates could be related by a set of
equations, to become known as the Lorentz transformations. These involve the
Fitzgerald-Lorentz contraction factor, F, which we've already met.
The Lorentz transformation for the times is:
t' = t(1-uv/c²)/ (1-v²/c²)^1/2.
(1-v²/c²)^1/2.
The velocity, v, stands for the relative velocity of two observers frames of
reference. The velocities, u or u', are the velocities of an object, seen by
observer 0 or observer O', respectively.
We have to bear in mind that the speed of light is so great in comparison with
our normal earth-bound movements, that it is in effect infinite. That being the
case, the Lorentz transformation, for two local times, reduces to just the one
("absolute") time, we are familiar with.
A Lorentz transformation applies to mass, also previously thought an
absolute. As a body approaches the speed of light, its mass increases. As this
speed is outside our normal experience, no such mass increases are observed.
But this phenomenum, as well as time dilation effects to particles normal
life-times, is regularly measured in laboratory experiments with atomic and
sub-atomic particles, moving very close to the speed of light.
In theory, a body could never reach the speed of light, because that would
involve acquiring infinite mass. Hence, the speed of light is a limiting
maximum on all objects with mass.
It turns out that momentum, or mass times velocity, has a similar form of
Lorentz transformation to that for distance measurements. Energy has a similar
transformation to that for the different times observers measure, in high
energy physics. (Given as a post-script to his 1905 paper on special
relativity, Einstein's E = mc² is the most famous consequence of these
transformations. Henri Poincaré also derived this equation in his close
anticipation of Einstein theory.)
The velocity, v, in the above Lorentz transformation of times, relates to
the difference between the observers two measured velocities, u and u'. But, as
things work out, it is generally not a simple subtraction between the two, to
allow for the fact that one laboratory is moving faster, relative to
another.
But, if one of the frames of reference is considered at rest, so the
velocity is zero, or u = 0, the velocity, measured in the other frame, u' = v.
The Lorentz transformation of times then reduces to the Michelson-Morley
calculation, modified by the contraction factor, F. For,
t' = t(1 + 0.v/c²)/F = t/F.
Two observers, with differences in relative motion, that are significant
compared to the speed of light, would observe different speeds in their clocks.
Moreover, these would be real effects, resulting in twins, say, ageing at
different rates.
The so-called "twin paradox" raises the question of why one twin, rather
than the other, since they are both in relative motion, should be the one to
age more slowly than normal. The retarded ager went off in the rocket, at a
velocity, that was a large fraction of the speed of light, and returned to
earth to find his twin long dead. The twins were just in relative motion --
most of the time.
The catch, that resolves the "paradox," is to do with the fact that the
rocket man would have to turn the rocket to return to earth, under-going the
kind of accelerative forces, not experienced on earth.
This is properly explained in popular physics books, such as by Paul Davies.
Richard Lung.
Early 2001; minor correction, sept. 2003.
Corrections, 16 june 2015.
To top.
Home page.
 (c²-u²).
(c²-u²).