Displacements from equilibrium.
Pascal's triangle is generated by the binomial
distribution. It displays endless mathematical relationships. It has been
said that when someone finds another such a property in this array of
numbers, the only person, that it comes as a surprise to, is its
discoverer.
Take any row of Pascal's triangle which is
generated by an expansion of the binomial theorem. Say, 1, 4, 6, 4, 1, and
multiply this respectively by from nought to four. This gives: infinity, 4,
12, 12, 4: that is to say another symmetrical distribution, always neglecting
the first term, infinity.
It is also possible to derive a symmetrical
distribution by dividing from one to five: 1, ½, ½, 1. 5, always neglecting
the last term. Larger distributions show more clearly that this fractional
distribution is somewhat exponential.
If you drew these
distributions, they would look like steep-sided bowls. A vertical line down
the middle would be like a mirror on one side to the other. You could call
this vertical axis, or y-axis, the mirror axis. The horizontal axis, or
x-axis, would be at zero level, the bottom of the bowl.
The vertical or
y-axis intersects the x-axis at zero, the lowest point of the bowl. The
x-axis to the right is positive, while the left is negative.
The positive and negative limits may be equal in
magnitude, called the amplitude, as in the crests and trofs of a wave of
equal height and depth. The zero level, equally in between, is called the
equilibrium and it corresponds to the level of a calm sea without any
waves.
See diagram of potential energy parabola:
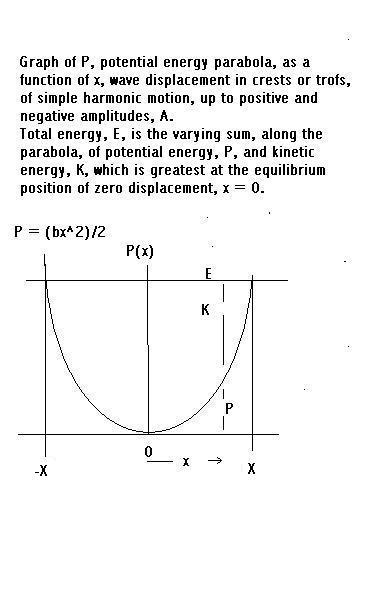
Having located the essential features
of a wave, in the bowl diagram, it is possible to redraw them as wave forms.
But these waves wouldn't look like the simple harmonic waves. The above is a
bowl diagram that shows the energy relations of harmonic waves but the curve
of the bowl is described by a parabola.
A parabola is a
function of a variable squared. Up till now, I have been thinking in terms of
the binomial distribution, because constituency seats and voters preferences
are readily modeled on this distribution. Now to turn to a different election
model.
To top
Equal representation
is served by proportional or elective quota counting. The Hare quota counts
how many voters are represented per seat, by dividing the total votes by the
number of seats in the parliament: V/S.
The Droop quota counts the proportion of votes
needed to elect each representative to a seat in a multi-member constituency.
The Droop quota is the total votes in the constituency, V/C divided by one
more than the number of seats in the constituency, S/C. That is:
(V/C)/{(S/C)+1}.
Assuming that there is only one constituency or C =
1, it is possible to treat these two quotas in terms of traditional
differentiation from first principles.
Let q stand for quota, so that (1):
q =
V/S.
Suppose a small change in the number of seats
produces a small change (given by sign, #) in the quota, so that
(2):
q + #q = V/(S+#S).
Therefore, (3):
#q = V/(S+#S) – V/S = -#S.V/S(S+#S).
Therefore (4):
#q/#S = -V/S(S+#S).
The value, #S, could be 1, as in the Droop quota.
Going thru the traditional differentiation procedure of reducing #S to a
limit of zero, and replacing the hash sign with a d-for-differentiation,
(5):
dq/dS = -V/S^2 = -q/S.
This is the so called derivative (the older term is
differential coefficient) of the quota with respect to the seats. It
represents a change in the quota with respect to a (zero-limit) change in the
seats. Or, the rate of change in the quota with the change in
seats.
The point is that the derivative’s independent
variable is a square and so it offers the prospect of a parabolic function,
which is what is required.
To top
It may be worth speculating what is the possible meaning of
differentiation from first principles that begins and ends in terms of the
Hare quota, with only the working bearing a passing resemblance to other
quotas like the Droop quota.
Going back to the early nineteenth century inspiration for proportional
representation, children queue behind their most popular candidates. The
longest queues elect their representatives to a limited number of seats on a
committee.
The lengths of the queues oscillate. Some children see their queue has
more support than their candidate needs to be elected, so they drift away to
swell the ranks of a next prefered candidate. Likewise some candidates cannot
win enough support to be elected, so their support drifts away to help a next
prefered candidate, who is nearly elected.
Eventually, the queues reach equilibrium. That is to say, all the winning
candidates have queues just long enough to elect them. That leaves a residue
of voters, not quite big enough or agreed enough to put a runner-up in
contention.
(A tie is possible and then the exclusion of one winning candidate is
decided randomly. For instance, by "taking the short straw" amongst a bundle
held out for the winners to chose.)
In a contest for only one seat, the winner needs over half the votes. The
minority have no choice but to be represented by the winner who they did not
vote for. That's not much of a choice and presumably many of them might not
think much of him as a second preference.
If the election is in a multi-member constituency, of, say, five seats,
then at least five-sixths of the voters may be represented. This leaves
another sixth of the voters unrepresented, if they prefered other candidates
than the five with most support.
Nevertheless, their situation is much rosier for choice than in a single
member constituency. The losing sixth of the voters might still decide they
prefered enough one or other of the five winners to join their queues, so
that all the voters might choose to show that they were satisfactorily
represented by the five winners.
If this were the case, then, in effect, the candidates have been elected not
only by the Droop quota, satisfying the minimum votes, each winning candidate
needs for election, but the winners have also been elected, in effect, by the
Hare quota, for maximum representation of the voters, or adequate
representation of all the voters.
Thus, differentiation that effectively winnows the Droop quota back down
to terms of the Hare quota may be expressing a reality about electoral
counts.
In abstract terms, the reality is that, as the number of seats grows, then
the change, of, say, #S = 1, becomes relatively less and less important, till
its relevance is vanishingly small: the (so-called zero limit-taking)
condition of differentiation.
An increase in choice from increasing number of seats in a larger
multi-member constituency may provide a a tipping point from the lower level
of equilibrium, provided by the Droop quota's minimum level of
representation, to the higher level of equilibrium, provide by the Hare
quota's maximum level of representation.
There is an analogy from physics of phase transitions, the abrupt changes
of form in matter such as from ice to water to steam. (This is the meaning of
the term, phase, in chemistry. The word, phase, is also used below but in its
mathematical sense.) This concept is widely used in physics, such as in
stages of cosmological evolution. In these examples, matter under-goes, stage
by stage, an increasing disorganisation, or "entropy", of its state.
The above electoral example has been considered in terms of increasing
order. The single member election has relatively high entropy or disorder,
because about half the voters, who did not first prefer the winning
candidate, only have a second preference, moreover that can only go to the
one winning candidate, who they may not be willing to rank as their second
choice.
On the basis of chance (as determined by the binomial theorem pattern 1/4,
2/4, 1/4) for a single vacancy, one quarter the voters equally prefer both
candidates; one quarter equally prefer not to vote for either candidate. The
two quarters are those voters who prefer one or other of two candidates.
Thus when US Presidential elections or single member constituencies have
only fifty per cent turn-outs, that may well reflect low theoretical
expectations from low-choice single vacancy elections.
With an increasing choice from more seats in larger multi-member
constituencies, the election may under-go a phase transition, in effect, from
a Droop quota election to a Hare quota election. This would be a state of
increased order, where voters preferences are sufficiently extended to the
point where everyone is represented by some winning candidate.
Of course, voters might be confused by too much choice, but such arguments
usually leave out the important consideration that voters can home-in on the
limited number of candidates who they will recognise as most representative,
before ordering their final choices.
Another possible quota, I christened "the Ross quota" is considered below.
(This supersedes my previous evaluation of a so-called Ross quota. See
foot-note 1.) This represents another possible equilibrium level in an
electoral system, where the requirement of equal representation is perturbed
by a conflicting, if lesser, requirement to make constituencies follow
natural community boundaries.
Like the Droop quota, this Ross quota makes for a somewhat lower, but still
stable, level of order than the Hare quota.
To top
The JFS Ross book,
Election and Electors has a particular affection in my memory, because it
converted me, as a student, from the complacency of my compatriots, to the
single transferable vote.
Later, I asked Frank
Britton, as secretary of The Electoral Reform Society, if they had a spare
copy and, amazingly, he posted me an old edition (not on their sales list of
literature).
JFS Ross gave the rule for cross-constituency
proportional representation in a single member system, with respect to
community boundaries.
It is not possible to
have PR within a single member constituency and the rule for PR within
multi-member constituencies is given by the Droop quota. The rule for PR
between constituencies, with no relaxation within or across constituencies,
is given by the Hare quota.
The Ross rule states that a single member
constituency must split equally in two, if its electorate goes so far above
the required average (given by the Hare quota) such that two constituencies
both half its size would be nearer to the required average in sizes of
electorate.
Suppose an electorate
of 36,000,000 has a Parliament of 600 seats. Thus a single member
constituency must have 60,000 electors, to give equal representation to
voters thru-out the nation.
The upper limit of
variation, from 60,000, is 80,000.This is because a constituency of 80,001 would be
more equitably divided into two constituencies of 40,000 and 40,001, since
the latter is closer to the 60,000 quota, than is 81,001.
In the 1950s, Ross complained that governments did
not understand this natural rule. And it’s still true now in 2011, where the
House of Lords has disputed (according to David Lipsey in a Guardian article)
the Tory coalition’s strict limit on variation to a mere 5%. The Labour peer
wanted it relaxing to 10%, which he said would not harm Tory representation.
On the contrary.
Even a 10% variation
is less flexible and more continually fragments natural boundaries and
messes-up local identities than the Ross rule. And that’s bound to stir up
more local inconvenience and discontent and acrimonious dispute. All because
the two parties, who can control a First-Past-The-Post single member system,
are jealous of any slight advantage between them, while tacitly agreed on a
system that under-represents or fails to represent anyone but
themselves.
However, the concern here is how to generalise the
Ross rule for multi-member constituencies with the same number of seats, S.
Also, a required average of votes per constituency, V/C. This is given from
the total votes in the nation divided by the number of constituencies.
In the traditional English two-member system. If total electors, V, = 36m.
and votes per seat, V/S = 60,000, and seats per constituency, S/C = 2, then
V/C = V/S x S/C = 120,00.
Let the least sized constituency be x voters, and
the most voters permitted be y. Let their equal difference in voters, from
the average of v, be z voters.
Therefore, v – z =
x
And v + z =
y.
The Ross rule shows
that the smallest permissible constituency in a single member system, is half
the size of the largest permitted.
The quota within a
single member constituency is also one-half, or fifty per cent of the voters
are needed to elect a candidate.
In other words, s/(s+1) = ½ in a single member
system, applies both to within-constituency representation and representation
across the single member constituency system.
Applying this Ross rule to multi-member systems,
that is two member systems or three-member or four-member systems etc, with
s, seats per constituency:
Then, x/y = s/(s+1).
It follows
that:
(v – z)/(v + z) =
s/(s+1).
Therefore:
vs + v – zs – z = vs
+ zs.
Or: v = 2zs + z.
Or: z = v/(2s +
1).
But the permitted variation in votes from the
smallest to the largest constituency is 2z.
And: 2z = 2v/(2s + 1)
= v/(s + ½).
This new quota
between the Hare quota and the Droop quota, I call the “Ross quota.”
Suppose the Hare quota, V/S = v/s, is 60 (which is
simpler to work than 60 000) then the required vote in a two-member system,
is s.v/s = 2 x 60 = 120.
The smallest or
largest permitted constituency is thus minus or plus z = v/(2s+1) = 120/(4+1)
= 24.
Therefore, smallest
constituency allowed is: 120 – 24 = 96. Largest constituency is: 120 + 24 =
144 voters.
This is a cross-constituency proportional representation of 96/144 = 2/3, as
expected for a two-member system, which also has a two-thirds PR within
constituencies.
Multiplying the Ross
quota by s, for: sv/(s+1/2), gives the minimum permitted constituency (e.g.
2x240/5 = 96). While multiplying by (s+1) gives the maximum permitted
constituency.
To top
An analogy between mechanical systems in simple harmonic motion and an
electoral system was ruled by certain considerations. The simplest case in
elections of displacement from equilibrium is perhaps given in the above
section on the Ross quota. This just involves some allowance made for natural
variations in the size of communities, such that some constituencies have to
be made larger and some smaller than strict proportional representation
requires.
Hence, the displacement had to be in votes per constituency above and
below the norm or equilibrium position. Note that in the above diagram, the
required average votes per constituency would be re-set to zero, so that the
displacement, above and below the norm, is only the number of votes per
constituency above or below that norm.
Mechanics, however, consists of two distinct systems, kinematics and
dynamics, which brings mass into the picture. To be true to the analogy with
elections, I had to make a distinction, essentially between representatives
and represented. This meant that the represented, as the voters, were
likened, literally, to "the masses."
Thus "kinematic" elections consist of representatives, S, and candidates,
K, as would-be representatives, just as kinematics in physics consists,
respectively, of time and space, but not the third quantity in the classical
physics triumvirate, mass.
My implicit definition of the candidates is as the minimum number of
voters. That is to say an election, in which there are only candidates
voting, is an election not swelled by any extra weight of voters, inessential
to the bare working of an election.
I have departed from strict analogy between classical physics and
elections, in that my definition of the equivalent term to mass, m, unlike
mass itself, is not a primitive term but a ratio of two terms, votes per
candidate. Instead, energy is chosen as the equivalent term to votes, This is
more in keeping with modern physics, in which energy is a rather more basic
concept than mass.
In the appendix, there is a table on the close relations between linear
motion and rotational motion. Essentially, rotational motion allows for a
return or repetition. In an election system, especially a uniform member
system, there is a repetition of constituencies. Northern Ireland or Ulster
has a six-member system. In other words, each constituency is a repetition of
six seats per constituency, and indeed repeats a proportional representation
of six-sevenths of the voters in each constituency.
Thus, the maths of rotation expressed number of turns or revolutions in terms
of constituencies, C.
Over the years, I have made several attempts at a good analogy between
maths of physics and politics. This pages endeavor is summarised in table
1.
Table 1: Maths of Physics and Politics.
| Physics: |
Politics: |
|
|
| x = Qr = 2πnr, length. |
K, candidates. (K = hpS, seats times parties times a constant,
h.) |
|
|
| y, length up to radius or (maximum) amplitude. |
k, candidates per constituency. (k = hps, constant times parties
times seats per constituency. Letting h = 1, p = s, k = s^2.) |
|
|
| r, radius or (maximum) amplitude. |
X, maximum variation from proportionly required average candidates
per constituency |
|
|
| t = Pn, time equals period multiplied by revolutions. |
S = 2πs.C/2π, seats (or representatives). |
|
|
| u = wr, velocity equals angular velocity times radius. |
K/S = k/s = hp. Candidates per seat. |
|
|
| Q = 2πn, angle. |
C, constituencies. |
|
|
| n, number of revolutions. |
C/2π, constituencies divided by 2π. |
|
|
| P, period or inverse frequency. |
2πs, 2π times seats per constituency. |
|
|
| w = Q/t, angular velocity (or angular frequency). |
C/S = 1/s, inverse of seats per constituency. |
|
|
| a = -yw^2, acceleration. |
-k/s^2 = -hp/s, or -1, if k = s^2, minus candidates per
(constituency seats) squared. |
|
|
| m, mass. |
M = V/K, voters per candidate. |
|
|
| p = mu, momentum. |
V/K(K/S) = V/S = q, vote quota. |
|
|
| b = mw^2, elasticity. |
M/s^2. |
|
|
| E* = (1/2)br^2, total energy equals kinetic energy plus potential
energy. |
V, total votes. |
|
|
| f = ma, force |
V/K(-K/S^2) = -V/S^2 = -q/S. |
|
|
*Note that energy can be expressed in terms of work done, which equals
force needed to move a mass body thru a given distance, or: W = fx.
The distance, x, can be considered as the velocity, from a start of zero
to a final velocity, u, over a given time, t. This implies, on average, a
velocity of half the final velocity, or u/2.
Thus, W = fut/2.
By Newton's second law, basic principle of mechanics, force equals mass
times acceleration, or, f = ma = mu/t.
Substituting this, W = fut/2 = fumu/2f = (1/2)mu^2,
which is the formula for the kinetic energy of a moving body.
The total energy, as shown in the diagram, equals the potential energy
plus the kinetic energy.
That is (1/2)br^2 = (1/2)mu^2 + (1/2)by^2,
where there is an elasticity constant, b, for instance governing the
degree of oscillation to a spring. The distance, y is up to the maximum
amplitude, r, of the oscillation. When y = r, the whole of the energy is
potential energy. That is the two points at the top of the parabola, in the
diagram, marking the furthest extents of the springs oscillation up and down.
There are any number of other examples: the amplitude might be the
furthest extents of the swing of a pendulum back and forth. Or, a ball at the
top of a bowl, before it is roled down, and upon reaching the top of the
other side of the bowl. Tho, this neglects friction impeding the swing
motions.
The kinetic energy, in contrast, is greatest, and consists of all the
energy, in the middle of the oscillation or the swing, marked by the zero
point, at the middle base of the diagram.
Following the rules of basic calculus, the potential energy can be reverse
differentiated ("anti-differentiated" or "integrated") with respect to
distance, y.
This transforms (1/2)by^2 into: by.
The kinetic energy also integrates with respect to y.
Thus: (1/2)mu^2 = (1/2)m(y/t)^2 integrates to: my/t^2 = -ma = -f.
These integrations or summings of the complementary potential and kinetic
energies are equal. Hence, f = -by.
That is to say that the force is proportional to the displacement, y, and
opposed to it, as shown by the negative sign. The force is always acting
towards the equilibrium or rest position, where displacement is zero, and
therefore the force is zero, between oscillations or swings.
The so-called simple harmonic motion, of an oscillating spring or swinging
pendulum or ball rolling up and down in a bowl, is given by the displacement,
y as a sine equation, such as: y = r.cosQ.
Or it could be, say, y = r.cos(Q + π/2) = r.sinQ. Or indeed any
so-called phase (call the phase: &), besides angle, π/2 radians,
could be used to signify the starting angle (*initial phase") of the wave
motion.
Sometimes the whole of the bracketed angle (Q + &) is called the phase,
with angle, &, called the "initial phase."
The maximum sine value is unity, which is when y = r, the (maximum)
amplitude. This is either the crest of the wave or its trof, the
corresponding negative displacement, from an equilibrium such as a calm water
level.
Given that y = r.sin(Q + &) = r.sin (wt + &),
the operation of differentiation with respect to time, t gives:
velocity, u = dy/dt = wr.cos(wt + &).
A further differentiation of velocity with respect to time, or in other
words, a second order differentiation of distance, y, with respect to time,
gives:
d²y/dt² = du/dt = a = -rw^2.sin(wt + &) = -yw^2.
From: f = -by,
m.d²y/dt² + by = 0.
Or:
d²y/dt² + yw^2 = 0.
This second order differential equation is the standard equation of simple
harmonic motion, which is solved in terms of the equation for y.
To top
The relevance of this basic physics for politics is that an election
system can be similarly measured.
An ethical force or moral imperative of proportionality attracts
oscillations or swings in sizes of constituencies back to equilibrium of the
required average.
For instance, you might have a constituency system in which there was a
seasonal shift of electorates from an equilibrium of equal constituencies.
This is not necessarily a single member system but could apply to
multi-member systems.
Suppose migrant workers doing seasonal work deplete one constituency to
augment another constituency, by an equal amount. This would represent a
seasonal swing in the size of these two constituencies, in principle, subject
to the same kind of (simplified) mathematics just discussed.
There would be, so to speak, a surplus transfer of voters to one
constituency leaving a deficit transfer from another constituency.
This surplus transfer, across constituencies, compares to the conduct of a
proportional count for an election within a multi-member constituency.
Candidates elected, with more votes than the quota they need to win a seat,
have the value of that surplus vote transfered to their voters next
preferences.
In accord with the democratic principle of one person one vote, the
transfering of surplus votes means that each voter, for a candidate elected
with a surplus, effectively has a proportionate fraction of their one vote
given as a "transfer value" to a next prefered candidate. The balance of that
one vote is kept, by the candidate elected with the surplus, and is called
the "keep value."
Akin to physics, the vote has an energy. The proportional count achieves
equilibrium when the surplus votes are transfered to prefered candidates
still in deficit of a quota.
Thus, the proportional count is not like a wave of uniform amplitude but a
damped wave down to equilibrium. Its equation modifies the uniform sine
equation with a damping coefficient in the form of an exponential function
with a negative index.
Before the votes are counted, they are all potential energy. The count of
the votes is how they move, or their kinetic energy. In common parlance, to
pass a motion means to take a vote. The most popular candidates with big
surplus votes will have the smallest keep values and the correspondingly
largest transfer values. That is to say their popular vote has the smallest
kinetic energy and the correspondingly largest potential energy for transfer
to next prefered candidates.
Simple harmonic waves are described by sine curves. These can also be
mathematicly expressed in terms of Euler formulas using an exponent with an
imaginary number in the index. That is of the form for a complex number, z =
r.e^iQ = x + iy = r(cos Q + i.sin Q).
I merely mention this, without attempting to explain it here, because, on
other pages, I have given election models of another type of exponential
function function, the normal distribution. At its simplest, this is of the
form, y = e^-(x²/2).
The various types of exponential function share the property that
conventional differentiation leaves the independent variable unchanged, tho
the coefficients are affected according to standard differentiation rules.
The wave equation, given above, involving a second order derivative, is
but one of several second order differential equations (which may be partial
differential equations having more than one independent variable) not only
with wave solutions but solving in terms of random or normal
distributions.
My treatment of the normal distribution was rather different to
convention, because I considered differential calculus on a statistical
basis. This allowed me to introduce a geometric mean form of differentiation,
which derived an exponential function, rather than just took it as found,
under traditional differentiation.
Appendix: corresponding strait-line and rotational motions.
I havent troubled to give electoral equivalents to all the physical
variables Ive mentioned. For instance, one physical concept not mentioned on
either table 1 or 2, that of Action, equals energy multiplied by time, might
be given an election equivalent of votes, times representatives, equals
number of preferences for representatives.
Some of the more complicated variables in table 2 might be compared
similarly in terms of election preferences. And there is always the fall-back
of primaries or candidates for candidature. But such ingenuity, at such an
early stage in a new subject, might not be particularly helpful.
Table 2: Physics of corresponding motions.
| Strait-line motion: |
Rotational motion: |
| distance, x = Qr |
angle, Q |
| velocity, u = wr |
angular velocity, w |
| acceleration a = αr |
angular acceleration, α |
| mass, m |
moment of inertia, I = mr^2 (for all mass on wheel rim) |
| force, f = ma |
torque, T = fr = Iα |
| kinetic energy, (Ek) = (1/2)mu^2 |
kinetic energy, (1/2)Iw^2 |
| momentum, p = mu = d(Ek)/du |
angular momentum, L = mur = Iw = d(Ek)/dw |
| impulse, change of momentum, ft |
angular impulse, change of angular momentum, Tt |
Note: This table is based on Milton A Rothman's The Laws of Physics.
The principal text consulted for this web page was Alonso and Finn:
Fundamental University Physics, volume 1. (This classic text was later
revised in one volume as "Physics" under the general editorship of Paul
Davies.)
Foot-note 1:
Or #S could be, say, 2, as in another quota, I formerly hazarded to call
the Ross quota (a term I now use for a new quota above). I relegated the old
page, on the former Ross quota, to My Archive. I don’t know whether it
contains a useful germ of truth or is just plain wrong! In any case, it was
not conformable to a parabolic function.
In this respect, my early work for a “Ross
quota” gave an unsatisfactory lop-sided answer but here I want to give an
equal amplitude variation limit to both smaller and larger than average
multi-member constituencies.
Richard Lung.
24 May 2011;
minor revisions, 16 June 2011.
To top
To home page
