To home page.
Links to sections:
Classical light signals vs quantum correlations.
Roger Penrose's popular accounts are manly attempts to give the curious,
like myself, a less vague idea of his profession's work. But in the midst of
all the technical glosses, he introduces us to the magic dodecahedra as a
recreational puzzle. Any one can enjoy this brain teaser 'without knowing a
proton from a crouton', to use another popular science author's expression.
This page proceeds in this spirit, with a minimum of back-ground
explanation.
Penrose beguiled readers of popular science, in his 1994 book, Shadows
Of The Mind, with the 'magic dodecahedra', here called the Penrose
dodecahedrons. They are Penrose's improved way of showing a contradiction
between assumptions of classical physics and quantum physics.
A crucial difference between the two view-points is in the role of the
physical observer. The classical physicist is a passive observer of an
objective reality. But the quantum physicist differently affects the reality he
observes by how he observes it. So, the quantum physicist's choice of
observation affects what he actually observes.
The Penrose dodecahedrons are about how the newer rules of quantum physics
cannot be explained away by the assumptions of classical physics. Take two
separate observers who make observations or measurements on two parts of a
conserved physical system of basic particles that have moved far apart. The
smallest constituents of matter are governed by the quantum rules. The effect,
of measuring one of the parts, should have a compensating effect on the other
part, no matter how far off, to conserve the system as a whole.
The classical view-point, first expressed in the Einstein-Podolsky-Rosen
paradox, asked how could this be? How could one part of the conservative
quantum system influence the other, if they were too far apart for a signal to
reach from one to the other, in time? ( This is bearing in mind that special
relativity tells us that no communication could take place faster than the
speed of light. )
But experiments, as by Alain Aspect, have supported the quantum rules,
involving 'non-locality', so-called because their influence goes beyond the
limiting principle of 'local causes' assumed in classical physics, and by
Einstein et al.
However, quantum theory does not violate special relativity, because there
is no way that measuring one part of a system, to influence its separated other
part, could produce a faster-than-light signal or communication, akin to morse
code. In The Emperor's New Mind, Penrose explains why the relationship
is not one of communication, while still admitting it is deeply puzzling.
Quantum rules of the 'magic
dodecahedra'.
To top of page.
Leaving aside the physical problems that gave rise to the Penrose
dodecahedrons, we may merely regard them as a recreational puzzle. Two
dodecahedrons represent the fields of choice of measurement open to two
observers. Penrose says one is here and the other is far away ( perhaps
galaxies away ) implying that light speed influences are not at work.
The twenty vertices, of both of the two dodecahedrons, each have a button.
The operating ( quantum ) rules are as follows.
The observer here and the observer far away may select any of the twenty
vertices, independently of each other. But they do not press the button on that
first vertex of choice. Instead, each observer presses the buttons, of the
three adjacent vertices, in any order he or she chooses. The observers'
respective orders of choice do not affect whether the bell rings. In any case,
the bell may not ring at all. If a bell rings, that ends the sequence of
button-pressings.
The ( quantum ) correlations or 'entanglements' that may arise between the
two observers' measurements, that is the button presses, are:
( 1 ) With reference to figure one, of the two separated but aligned
dodecahedrons, suppose the observer here and the observer far away select
diametrically opposite vertices of their respective dodecahedrons, from the
choice of 20 vertices each of them could possibly make. Each observer may
press, in any order - depending on whether a bell stops further pressings - up
to all three adjacent vertex buttons to their first selected vertex ( whose
button is not pressed ). A bell may only ring if the button vertex pressed, on
one dodecahedron, is diametrically opposite to a pressed button vertex on the
other observer's dodecahedron.
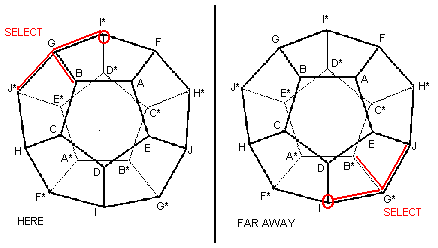
Figure 1: diametrically opposite vertices ring together, if at all.
In this example, the observer, here, selects vertex G and the observer, far
away, happens to select its diametric opposite, G*. From their respective
adjacent vertex preferences, the figure shows bells ringing at diametrically
opposite vertices I* and I:
( 2 ) With reference to figure two, the two observers happen to select
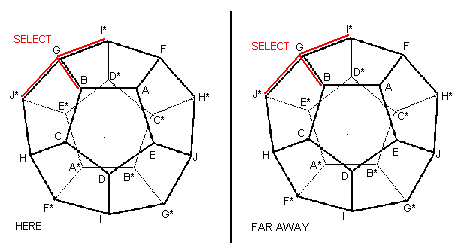
corresponding vertices. Whatever orders they happen to choose to press their
respective three adjacent vertex buttons, a bell will ring on at least one of
the six vertices the two observers can choose between them.
Figure 2: At least one of the six adjacent-to-select buttons rings.
Classically assumed independence from
quantum correlations.
To top of page.
Classical physics assumes that the only possible kind of influence between
the two dodecahedrons is of the nature of a signal. This could not out-pace
light, which has not had time to communicate the observed influences.
Therefore, the classical reasoning is that the dodecahedrons are independent.
For an observed dodecahedron, it would follow that (1) it has already been
determined which buttons ring or not.
The classical absence-of-influence assumption implies a certain vertex is a
pre-arranged bell ringer, in context of figure one: if one of the here
observer's three button presses ( in whatever order ) rings a bell, then the
far observer's first of three vertex button presses must also ring, if
it happens to be the diametric opposite of the here observer's ringing
vertex.
(2) No next-to-adjacent buttons can both be ringers. Remember, once a bell
rings to one of the selected vertex's three adjacent vertex buttons, that stops
the operation of pressing the three, in one's chosen order. With regard to
figure 1, if two next-to-adjacent buttons were both bell ringers, then the
order, one observer pressed them, would make a difference to which bell rings,
if the other observer's select button was the diametrically opposite one on his
dodecahedron.
(3) On, say, the here dodecahedron, for a selected vertex, at least one,
either, of its three adjacent vertices' buttons, or, of its diametrically
opposite vertex's three adjacent buttons, must ring.
The third point follows from combining the two conditions illustrated in the
two figures. Re figure 2, if the far observer selects the corresponding vertex
to the here observer's choice, then either one from the near or far set of
three adjacent buttons must ring. If none of the near set rings, then one of
the far set must ring. But then, re figure 1, that ring would be liable to set
off a matching ring from a vertex that corresponds to its diametric opposite
vertex on the near dodecahedron.
Disproof of independence from quantum
correlations.
To top of page.
Penrose goes on to show that the three classical conditions dont hold
together. Condition (1) of pre-assigning all the dodecahedron's vertices, as
ringers or not, cannot be made to work under conditions (2) and (3).
Penrose says someone else may think of a 'snappier proof'. It's definitely
not one 'straight from the book', as Paul Erdös would say.
Figure 3: dodecahedron with inscribed cube.
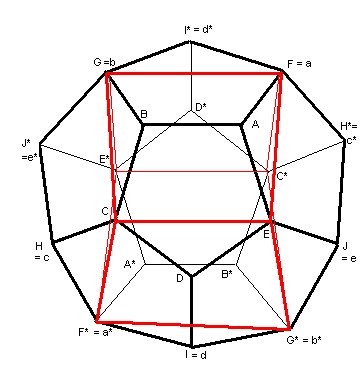 |
Re Penrose's 'non-locality' proof: The vertices are given
Penrose's letters: A to E are the vertices of a pentagon facet. F to J
are their adjacent vertices. A* to J* are their respective antipodal -
or diametrically opposite - vertices.
Re the preference permutations of 5 choices: Some vertices
show equivalent labels to Penrose's, for the next section, on how a
dodecahedron represents the 120 permutations of 5 choices.
Apologies for the Escher-like appearance of the inscribed red cube,
which has five possible orientations in the dodecahedron - just one
cube representing the 24 permutations of 4 choices. And 5 times 24
derives the 120 permutations of 5 choices. )
|
Penrose's demonstration is as follows ( see figure 3, re Penrose's
'non-locality' proof ):
From condition (3) at least one vertex must ring. Assume this is A. Suppose
neighboring vertex B also rings. If so, condition (2) forbids all A and B
vertex's ten surrounding vertices ( C, D, E, J, H*, F, I*, G, J*, H ) to ring,
because they are all next-to-adjacent to A or B.
Condition (3) requires of the anti-podal pairs, H and H*, that at least one,
of their two sets of three adjacent pairs, rings. Of these six, only F* or C* (
or both ) are not already ruled out as ringers. Likewise, taking the anti-podal
pairs, J and J*, only their adjacent vertices G* and E* ( or both ) are not
already ruled out as bell ringers. But G* and E* are both next-to-adjacent to
both F* and C*. So, condition (2) also rules them out as bell ringers.
Thus a pair of ringing vertices will not meet the conditions: B, as well as
A, cannot ring. A must have non-ringing adjacent and next-to-adjacent vertices
( B, C, D, E, J, H*, F, I*, G ). From condition (3), one vertex must ring of 6
adjacents to the anti-podal pair, A and A*: B*, E*, F* are remaining
possibilities.
If F* is the bell ringer, adjacent H and next-to-adjacent E* and G* do not
ring. But anti-podal vertices J and J* now have no bell ringers among their six
adjacent vertices. The same reasoning applies to E* as the bell ringer with
respect to anti-podal pair H and H*; and B* as the ringer with respect to pair
I and I*.
This completes Penrose's proof that one observer's vertices pre-arranged to
ring, because ( light-signal ) independent of the other observer's
dodecahedron, does not work under the rules of quantum correlation between
parts of a conservative system.
To top of page.
Classic Greek geometry proves there are only five regular solids. Three of
these have triangular facets ( 4, 8 and 20 in number ). The other two are the
cube, with 6 square facets, and the dodecahedron, with 12 pentagon facets.
The dodecahedron is familiar in the black and white chequered facets of the
soccer ball.
Murray Gell-Mann's The Quark and the Jaguar ( also reviewed )
features systems analysis. The most interesting systems are complex enough to
carry useful information but regular enough to make it of general application.
The dodecahedron is rather like that.
An electoral interpretation of the Penrose dodecahedrons depends on the
geometry of regular solids serving as illustrations of permutatons of choice.
The basic idea can be given by a triangle, whose corners or vertices are
labeled A, B, C. These letters might represent three candidates to choose from.
You could put this triangle on a pivot and spin it from a fixed position or
origin.
Say, corner A is at that origin and anti-clockwise round the triangle you
read off the vertices, A, B, C. This represents one of the six possible orders
of choice or preference permutations.
Now rotate the triangle anti-clockwise from A at the origin to B at the origin.
This yields a second order: B, C, A. Another anti-clockwise turn to C at the
origin yields: C, A, B.
Repeat this process in the clock-wise direction for the other three possible
preferences: ACB; BAC; CBA.
The 24 possible permutations of choice for four candidates, A, B, C, D, can
be represented by a cube. The five possible orientations of a cube inscribed in
a dodecahedron can represent the 120 possible orders of choice for five
candidates, A, B, C, D, E.
Permutations of choice are given by the factorial of the number of choices ( or
candidates ). Three choices means factorial three ( 3! ) or six permutations:
3! = 3.2.1 = 6. Factorial four, 4! = 4.3.2.1 = 24. Factorial five, 5! =
5.4.3.2.1. = 120.
All the permutations of choice are equally valid possibilities. Likewise,
the six operations, on the triangle, used a standard procedure of position and
direction to represent each of the six permutations. This is still true of
representations using three-dimensional regular polygons.
With reference to figure 3, see how the red cube represents 24 permutations
of four choices, F, G, C, E. Using the equivalent labels shown in the figure 3:
F = a, G = b, H = c, I = d, J = e, F* = a*, G* = b, H* = c*, I* = d*, J* = e*.
FGCE = abCE are also the corners of the cube's near face ( marked in thick red
lines ). Its opposite face ( in thin red lines ) is marked C*, E*, a*, b*. The
asterisked corners still represent the same choices, say of candidates, C, E,
a, b. The reason why we have this duplication of choices is that it takes three
cube faces, in three dimensions, rotated, clock-wise and anti-clockwise, to
represent all 24 permutations of the four choices.
Just as a pivot was put thru the triangle to turn out permutations of its
three corners A, B, C, so a pivot or axis can be put thru each of three
mutually perpendicular faces of the cube.
Take the red cube's front face, E, C, a*, b*. Four anti-clockwise turns
yield the four permutations: ECa*b*, b*ECa*, a*b*EC, Ca*b*E. Four clockwise
turns yield their reverse permutations: Eb*a*C, CEb*a*, a*CEb*, b*a*CE.
Now take the red cube's top face EabC, again working from the E corner or
vertex, anti-clockwise to yield four more permutations: EabC, CEab, bCEa, abCE.
Four clockwise turns again yields their reverse permutations: ECba, aECb, baEC,
CbaE.
The red cube's third dimension, sideways does not show up properly on figure 3.
But yet again starting at E anti-clockwise, it is Eb*C*a. Its four
anti-clockwise permutations are Eb*C*a, aEb*C*, C*aEb*, b*C*aE. Its four
clockwise perms are: EaC*b*, b*EaC*, C*b*Ea.
This completes the 24 possible permutations of ECa*b*, which, notice,
encloses the D vertex. D belongs to the dodecahedron facet ABCDE. The red cube
can be oriented to enclose each of these five corners, A, B, C, and E, as well
as D.
BEc*d* encloses A. As above, we can cycle these four labels to get four
permutations and then get four more permutations by reversing them.
The other two cube faces which meet at vertex B can be derived by a rule
implicit in the relation between the three faces meeting at vertex E:
For the second face, ECa*b* transformed to EabC, so transform BEc*d* into BcdE.
For the third face, ECa*b* transformed into Eb*C*a, so transform BEc*d* into
Bd*E*c.
Thus the orientation of the cube, with respect to the top dodecahedron facet
at A, yields three square faces meeting at vertex B. These three faces each
have four corners which yield four permutations and their four reverse
permutations, totalling 24 possible permutations.
The cube similarly oriented to B, yields three more square faces meeting at
vertex C; cube orientation to C yields three faces meeting at D; cube
orientation to D yields three faces meeting at E; cube orientation to E yields
three faces meeting at A.
Thus the five possible cube orientations to dodecahedron facet ABCDE yield 5
times 24 equals 120 possible permutations of those five choices. See table
1.
Table 1: 15 key perms yield 8 perms each for 120 perms of 5
choices.
| The first column's single letters remain first choice in
their succeeding three rows of 4 perms when cycled to produce 4 perms
each. When these 4 perms are each reversed, the single letters become
last choices. |
| A |
BEc*d* |
BcdE |
Bd*E*c |
| B |
CAd*e* |
CdeA |
Ce*A*d |
| C |
DBe*a* |
DeaB |
Da*B*e |
| D |
ECa*b* |
EabC |
Eb*C*a |
| E |
ADb*c* |
AbcD |
Ac*D*b |
Richard Lung
To top of page.
Penrose dodecahedrons: (2) 'electorally'
interpreted.
To home page.


