The Minkowski Interval (1908): described.
The Interval: diagram explained.
The Interval: Phase-different frames of reference.
"The Interval" of Minkowski is an extension of Euclid geometry for making measurements in three dimensions of space. An example, of Euclid, is measuring the height, length and breadth of a box-room from one of its corners. Minkowski treated time as a fourth dimension of space and integrated it into a four-dimensional Euclidean space-time geometry.
The advantage of this new mathematical formalism was that all observers different space and time measurements could be re-stated in a formula, known as "the Interval," a constant spatio-temporal measurement, which is the same for all observers. This reflects the fact that, tho the observers were using their own co-ordinate systems, they were all seeing the same event.
(The qualification needs to be made that the Interval only applies to observers moving in "uniform relative motion." To remove this arbitrary restriction, Einstein had to come up with his "principle of equivalence" of acceleration to gravity, which was the basis of a general theory of relativity.)
The only mathematical difference between the three spatial dimensions and the one temporal dimension is that time units are multiplied by the mysterious square root of minus one (given the symbol i).
We may see solid shapes changing in time. We may imagine our three dimensional world in a historical perspective. However, the three spatial dimensions are essentially the same in character and we need only one of them to show how the time dimension relates to spatial measurement. One space co-ordinate, x, and one time co-ordinate, t, can be represented, diagrammatically on a two-dimensional page.
So, we relate the spatio-temporal measurements of two observers, working in two different places and times, and therefore with two different co-ordinate systems: the x and t system, of one observer, is distinguished from an x' and t' system, of another observer, with different space and time measures, distinguished by indices. Of course, both systems have two other dimensions of space to consider. For simplicity, we've assumed their measurements dont differ in that respect. In other words, their space measures on the y and z dimensions are equal, or y = y' and z = z', comparing the two observers co-ordinate systems.
The Interval derives the Lorentz transformation for time, and for space, in much the same sort of way, partly with the use of trigonometry. The Lorentz transformation can be expressed as an equation of one observers time, t', or the other observers time, t. Likewise, for their respective distance measurements, x and x'.
The Interval points to a space-time co-ordinate position, that is both x + ict and x' + ict'. These four values are essentially the Lorentz transformations, we've just been speaking of. Here, they form two different sets of co-ordinate axes, that are the two observers frames of reference.
Using trigonometry, the Interval allows observers varying space and time measures to be drawn as the varying opposite and adjacent sides, of a right-angled triangle, with respect to one of the other two angles. For instance, a more acute angle makes the opposite side, of the triangle, relatively short. These opposite and adjacent sides will vary according to the rotation of the hypotenuse, as the constant radius of a circle.
Any position on the circle boundary, that the radius points to, is a given space-time position, perhaps marking some mutually observed physical event. Any number of observers can choose different ninety degree co-ordinate systems of space and time, on the circle, given that their axes all share the same origin at the centre of the circle.
With these different anglings of their rectangular co-ordinates, they can all measure any one given space-time position on the circumference. Their respective axes will all show different space-lengths and different time-lengths in relation to that common sighting. In effect, each co-ordinate system is like a triangle with varying opposite and ajacent sides for varying distances and times.
But all these different triangles have the same hypotenuse. By Pythagoras theorem, their varying lengths, on different space and time axes, add up to the same unitary space-time measurement, given by the length and direction of their shared hypotenuse, as a constant radius pointing out any given space-time event on the circle circumference.
This space-time radius vector is "the Interval." (A vector means a [magnitude of] length in a pointed direction.) The Interval applies not only in one dimension of space and one dimension of time. For example, making measurements in two dimensions of space, as well as one dimension of time, the radius could vector-in on a given three-dimensional space-time position, represented as a point on a sphere, instead of a circle.
Pythagoras theorem, for finding the Interval as hypotenuse, extends to apply to three or more dimensions.
For the four-dimensional space-time treatment, the Interval would, presumably, be a radius 4-vector pointing out a position on a four-dimensional hyper-sphere, whatever that is - something beyond the imagination of our three-dimensional experience, perhaps.
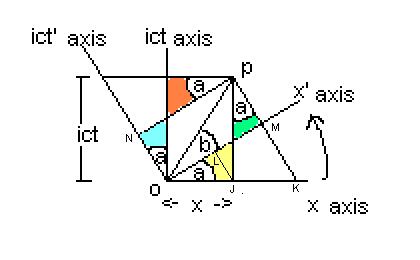
Having explained the Interval in words, simple equations will give a more precise idea, with the help of the following diagram.

The Interval is given by the radius vector, OP, which is the hypotenuse of triangulations based on both co-ordinate systems. Thereby, the point, P, is located by both systems, the two sets of co-ordinate positions, x + ict and x' + ict', differently representing the same position.
The diagram shows, schematically, the essential difference between two observers measuring, in space and time units, the same event at position, P. Special relativity recognises local ruler or "rod" lengths and local clock rates. These correspond to the different co-ordinate systems the observers are working with.
On the diagram, the two observers each have a pair of ninety-degree axes.
One observer measures distance and time, in units x and t.
For time to be in the same length dimensions as x, time, t, is multiplied by c,
the constant speed of light. The other multiple, i, is sometimes described as
an operator. Just as the plus sign, +, means the operation of adding, so the i
sign can mean the operation: turn thru ninety degrees.
The other observer measures distance and time, in his units, x' and t', on
his x' and ict' co-ordinates.
The diagram shows the only real difference between this co-ordinate system, and
the other, mathematically, is that it is a turn, thru angle, a, away from the x
and ict axes system.
Of the four angles, a, on the diagram, I refer to the angle a, at the origin, O, and marked by the up-wards curling arrow, to show angle, a, is the angle of tilt between the (x, ict) right-angled co-ordinate system and the indexed co-ordinate system. The triangle for this particular angle, a, is color-coded yellow in the diagram.
Position, P, where the event is, that the observers are both measuring, is equally well located by one set of axes as another: x' + ict' marks the spot as well as x + ict. There is no privileged or prior frame of reference. The frames are "only relative" to each other. This would be true for any number of observers, with their own co-ordinate frames, at varying angles, about origin, O, from each other.
They would all have in common what these two observers have. They would share the same hypoteneuse, OP. This is "the Interval," a constant space-time measurement, that all observers (in uniform relative motion) can agree is the same measurement of the event at P. Yet, the observers arrive at the Interval from their different measurements of space and time, treated by each observer as separate measurements on a separate space axis and a separate time axis.
It is in the context of the Interval, that special relativity is about an integrated concept of "space-time."
The value of the Interval can be found from any co-od. system. Taking the (x,t) system, and using triangle OPJ: As shown on the diagram, the length of OJ is x = ut. The length of JP is ict. By Pythagoras theorem, the length of the hypotenuse, OP, which is the Interval, is found from: (OP)² = x² + ( ict )² = t²(u²-c²).
Usually the Interval is left in this squared form.
Taking an other observers system, (x',t'), the Interval can be found by the same procedure, this time using triangle OPM. The diagram shows that, as this other right-angled triangle has the same hypotenuse, OP, the Interval, as such, is obviously the same value.
In the indexed co-ods., the Interval squared equals t'(u'²-c²).
Usually, text books leave the Interval, I, in terms of the hypotenuse squared, while showing the equivalence of two different frames of reference, like so:
I² = t²(u²-c²) = t'(u'²-c²).
The Interval is a rotatable radius (tho, the diagram doesnt include a full circle, showing the origin, O, at its centre, and the Intervals particular position, given at P, as on its circumference). No mathematician, I still couldnt help notice that such a radius vector draws out waves, in either time or space, or both. Such wave equations have independent variables of up to three dimensions in space and one independent variable for time, on the other side of the equation. Both sides act on a dependent variable of wave displacement. The Interval seems rather like this classical wave displacement, acted upon by four separate components of space and time, but summarising them mathematically as a unified space-time measurement.
The Interval is a constant for any given space-time event but becomes a variable once one considers it moving thru a circle or sphere of events (or 4-D space-time hyper-sphere of events).
The Interval was marked at P, on the diagram, by two observers co-ordinate systems. But, in the process, it was also marked by two different kinds of co-ordinate system: rectangular or rectilinear co-ordinates and polar co-ordinates.
The Interval was described as a space-time vector, giving both length (including length of time) and direction. In our two-dimensional example, any point on a plane, or sheet of paper, could be indicated by this means.
The same can be done with complex numbers. These are an extension and completion of the number system, with rules of counting somewhat different from traditional numbers. Complex numbers are taught to young children as part of the "new maths" in schools.
The two observers each described the position, P, by a complex number: x + ict or x' + ict' (which may be set equal to z and z', respectively.) This meant that, in this instance, the two complex numbers were equal. These complex numbers are in the system of rectilinear co-ordinates. This works like a net. Depending on how fine the net is, you can mark any position, on a stretch of ground it covers, by which node or knot in the net lies over it.
But the Interval diagram also used another kind of co-ordinate system, because the two rectangular co-ordinate systems were related to each other, by sharing the same origin, and having their axes turned at a given angle to each other. They also shared the same hypotenuse, a radius vector, which was the Interval itself.
A co-ordinate system which measures, in this case a plane, by sweeping out an angle, in a circle, with a radius, is called a polar co-ordinate system. The origin is the "pole."
We can also express z and z' in polar co-ordinates. From the Interval diagram, let the radius, from the origin, O, pointing to position, P, be called r.
Then, cos(b+a) = x/r.
i.sin(b+a) = ict/r.
z = x + ict = r{cos(b+a) + i.sin(b+a)}
Thus, z is expressed both in rectangular and polar co-ordinates.
Similarly for z':
cos(b) = x'/r.
i.sin(b) = ict'/r.
And z' = x' + ict' = r{cos(b) + i.sin(b)}.
A well-known result says the trigonometrical terms can be replaced by an equivalent term, using the exponent (usually written "e" or "exp").
( So, complex number, z', equals radius, r, times the exponent, e, to the
power of an index, which is the operator, i, times angle, b.
For, z, the only difference is that the angle in the index is not angle, b, but
angle, b+a. )
These various expressions are standard text book solutions for z or z' as a wave form, in a so-called wave equation. Z can be imagined as the point, P, in the Interval diagram, moving around the circle, whose circumference it is on. This circular motion can be charted, horizontally on a graph, as a wave motion. The horizontal axis can represent the lapse of time or distance.
The (positive part of the) graphs vertical axis represents the height of the wave. Its full height or crest is called the amplitude. It is the same length as the radius. When the radius reaches the northern vertical position, on the Interval diagram, this corresponds to a crest of the wave. From there, for every full circle, the radius sweeps out, the graph of the wave reaches another crest.
Our Interval diagram only shows the positive quadrant of the circle co-ordinates. When the radius reaches the southern vertical position, where the ict-axis has changed to -ict on the circle, this corresponds to a trof of the wave being drawn out on the graph.
This is why a solution of the wave equation is typically given as a function of: x ± ct.
Both z and z' mark an event, P. Presumably, the two observers could both track P, if it were to describe a circle in space-time, on the Interval diagram. In doing so, the two observers would trace out their respective z and z' wave forms on the graph. But these wave forms would not be synchronised, because there is a difference of angle, a, between their co-ordinate systems.
This difference of angle is called the phase. A difference of phase, between physical waves, is responsible for interference effects, such as the patterns made by colliding water waves.
On the Interval diagram, an angle, a (color-coded yellow) shows the two observers spatial axes, x and x', out of phase to that degree. Consequently, their temporal axes, ict and ict', are also out of phase by angle, a (color-coded green).
In general, this situation applies to the Interval as a four-dimensional space-time. So, you could characterise different observers, of relativistic effects, as having co-ordinate systems, with space-time phase differences from each other.
It is only a phase they are going thru.
For the Michelson-Morley experiment, I relied on:
Sir James Jeans, The New Background Of Science. Scientific Book Club, 1945.
Isaac Asimov, Asimov's Guide To Science, Vol. 1, The Physical Sciences. Penguin 1972. The appendix also contains a simple derivation of E = mc².
Arthur Beiser, Concepts Of Modern Physics. McGraw-Hill 1973. Chapter one.
For the Lorentz transformations, I cannot remember the first book that interested me in them, but I have read appreciatively, on the way:
Milton Rothman, The Laws Of Physics. Penguin 1963.
Allan M Munn, From Nought To Relativity. Allen and Unwin 1974.
Paul Davies, Space And Time In The Modern Universe. Cambridge University Press 1977. This carefully explains away the twin "paradox." Davies has written a good many popular physics books since then, most of which I read.
For the Minkowski Interval, I relied on:
George E Owen: Fundamentals of Scientific Mathematics. The John Hopkins Press 1961.
Richard Lung.
2001; revised, 16 june 2015.