Changing the co-ordinates to the graph of the Fibonacci series.
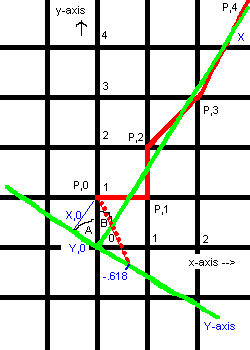
The progress of the red zig-zag line, which marks the successive pairs of the series, is directly measured by the green co-ordinates, as such, the so-called eigenvectors.
Disclaimer: The following three web pages were written by an outsider to mathematics. They have not been independently checked. They are only a personal attempt at understanding, tho hopefully helpful to others.
( Notation:
subscripts to a term are shown by a comma in between the term and the symbols
usually subscripted: x,n means the n-th term of x instead of the convention
that n is a sub-script.
Super-scripts, such as powers, are shown by a quotation mark between the term
and its power: x'n means x to the power of n. But the usual notation x² is
used for x squared. )
Links to sections:
The Fibonacci series occur in natural forms, such as the arrangement of pine-cone or pineapple whorls or sun-flower petals. It has been widely studied by mathematicians.
Solving the formula for the Fibonacci series is perhaps as easy a way as any to understand certain equations of wide-spread use in science. The series starts with a pair of numbers, most simply 0 and 1. They are added, to produce the next number in the series, which is added, in turn, to the previous number, and so on:
0 + 1 = 1; 1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8; etc.
That is, the Fibonacci series goes: 0, 1, 1, 2, 3, 5, 8, 13, 21, etc.
A graph can be drawn of the added pairs, as the x and y axes, respectively. The x values coincide with the whole series, and the y values with all but the first term, zero.
 |
The progress of the red zig-zag line, which marks the successive pairs of the series, is directly measured by the green co-ordinates, as such, the so-called eigenvectors. |
Finding the formula for the series amounts to this: given any first pair of numbers, a,0 and a,1, ( most simply 0 and 1 ) what is the value of the n-th term, a,n? Here, a,n can mean the tenth, nineteenth, seventy-first, or any other order of term in the series. It coincides with the n-th term of the x ordinate, x,n. In other words, a,n = x,n.
( The normal notation, for the order of term, follows series letter a, or x, with a sub-script number or sub-script letter n. )
The graph's red line shows the successive pairs of the series. They get
closer and closer to the X-axis of a new co-ordinate system ( drawn in green
). This new ordinate conveniently shows the limit to which the series
approaches for larger and larger values of the pairs in ratio, y/x: 1/1, 2/1,
3/2, 5/3, 8/5, etc. This limit is 1/2( 1 +  5 ) or about
1.618. The X-ordinate has the equation y ~ 1.618x, in the original
co-ordinates.
5 ) or about
1.618. The X-ordinate has the equation y ~ 1.618x, in the original
co-ordinates.
The other new ordinate, Y, has the equation y = - 0.618x. The negative sign
is with respect to the fact that, with each step of the series, the red
zig-zag skips from positive to negative sides of the new, Y-axis. This also
allows the zig-zag to be traced back ( see the dotted red line on the graph )
to - 0.618 on the Y-axis.
Taking the diminishing zig zag as the crudest representation of a damped wave
or lessening oscillation, this is its starting point leading directly to the
original maximally displaced amplitude of the wave, before its energy is
gradually lost in the damping down, as by a shock absorber.
Finding the limiting value of the series is established by a standard procedure, involving the 'characteristic equation': T² - ( a + d )T + ( ad - bc)I = 0. ( Text-books commonly supply a proof of this equation. )
Simply substitute the first two pair numbers, 0, 1 and 1, 1, of the series into a, b, c, d, respectively: T² - ( 0 + 1 )T + ( 0x1 - 1x1 )I = 0. And use the formula for solving quadratic equations ( where the letters a, b, c, are put to a different use: a is the coefficient of T², b is coefficient of T, c is coefficient of I, for Identity, which is essentially just a unitary term ). So:
T = ( - b ±  ( b² - 4ac ))/2a. = 1/2( 1 ±
( b² - 4ac ))/2a. = 1/2( 1 ±  5 ) ~ 1.618 or - 0.618.
5 ) ~ 1.618 or - 0.618.
( Notice that we needed two distinct roots for two new co-ordinates. )
The T is for transformation that tells how much each member of a pair gets
simply expanded or shrunk, in a straight line, with the next step of the
series, in this new co-ordinate system. In other words, if X, Y are a pair and
X*, Y* are their next steps or succeeding transformations, then X* ~ 1.618X
and Y* ~ - 0.618Y. Co-ordinates which have this simple linear property are
called 'eigenvectors'. And their magnitudes, or the amounts they get expanded
or contracted, are called their 'eigenvalues'.
( These central terms of 'linear analysis', the once 'modern' mathematics, of
which Sawyer spoke, haunt texts of mathematics and modern physics. )
In the new co-ordinates, the first pair of the Fibonacci series, X,0 and
Y,0, may be found as follows, with reference to the above graph. The tangent
of angle B is in the ratio of 1 over 1.618, or, tan B = 1/1.618. Therefore,
angle B = 31.718 degrees. Subtract from 90 degrees to find angle A = 58.232
degrees.
Sin A = X,0/1 = 0.85.
Cos A = Y,0/1 = 0.526.
All the succeeding values of X and Y may be found, respectively, by
multiplying these initial values by the new co-ordinates' eigenvalues, to the
power of n ( here signified 'n instead of with index or super-script n ) where
n is the order of the term in the series being sought. In other words, X,n =
X,0.( 1.618 )'n. And Y,n = Y,0.( - 0.618 )'n.
See table one ( comparing with the graph of both co-ordinate systems ):
| n | x,n | X,n | y,n | Y,n |
| 0 | 0 | 0.85 | 1 | 0.526 |
| 1 | 1 | 1.375 | 1 | - 0.325 |
| 2 | 1 | 2.225 | 2 | 0.201 |
| 3 | 2 | 3.600 | 3 | - 0.124 |
| 4 | 3 | 5.825 | 5 | 0.077 |
| 5 | 5 | 9.426 | 8 | - 0.047 |
If the diminishing zig-zag were considered as a simplified model of a damped wave or oscillation petering out, the X-axis is the equilibrium line to which the disturbances finally settle. Whereas the Y-axis measures the amplitudes of the vibrations as their crests and troffs, about either side of the X-axis, get smaller and smaller.
Table two shows how to convert the n-th term back into an original x-axis
reading, x,n. That is any term in the Fibonacci series:
x,n = C( 1.618 )'n + D( - 0.618 )'n, where C and D are constants.
This is the form of a solution to a second order equation. Indeed, the damped wave equation is a second order differential equation.
The constants are determined by the first two x terms, 'the initial conditions', of the series, here zero and one.
Taking x,n as zero,
0 = C( 1.618 )'0 + D( - 0.618 )'0 = C + D.
So, C = - D.
Taking x,n as one,
1 = C( 1.618 )'1 + D( - 0.618)'1.
Substituting C for - D,
1 = C( 2.236 ). So, C = 0.447. And D = - 0.447.
Therefore, x,n = ( ( 1.618 )'n - ( - 0.618 )'n )0.447.
This is the Fibonacci series formula, that we have been looking for. See table
two for examples.
| n | ( 1.618 )'n | - | ( -0.618 )'n | = | Times 0.447; x-values. |
| 0 | 1 | - | 1 | 0 | 0 |
| 1 | 1.618 | + | 0.618 | 2.236 | 1 |
| 2 | 2.618 | - | 0.382 | 2.236 | 1 |
| 3 | 4.236 | + | 0.236 | 4.472 | 2 |
| 4 | 6.854 | - | 0.146 | 6.708 | 3 |
| 5 | 11.089 | + | 0.090 | 11.179 | 5 |
The Fibonacci series is a difference equation, say, x,n+1 - x,n = x,n-1. For instance, from the above table of x-values: 1 - 1 = 0, 2 - 1 = 1, 3 - 2 = 1, 5 - 3 = 2, etc.
Suppose these are differences between distances each covered in unit time, h = 1. ( How closely the difference equation approximates the differential equation depends on how finely the time is measured. But h might mean an interval of space. For instance, wave crests may be a spatial function of the uniform wave-lengths between them, as well as forming periodically in time. Instead of h = 1 hour, measurement over minutes, h = 1/60, is more accurate, as measuring over seconds, h = 1/360, is more accurate still. But this is not the concern here. )
So , differences in distance, x,n+1 - x,n, and x,n - x,n-1, covered in time, h, are ( x,n+1 - x,n )/h and ( x,n - x,n-1 )/h. This is known as first order change, like velocity, as change in place over time.
A second order change is a change in a change of values, like acceleration,
as a change in a change of place over time, or a change in velocity over time.
This might be ( 5 - 3 ) - ( 3 - 2) = 1.
Each difference ( x,n+1 - x,n )/h, ( x,n - x,n-1 )/h is, in turn, subtracted,
and divided by h, again, resulting in ( x,n+1 - 2x,n + x,n-1 )/h². A second
order term, like this, is the highest order term in a second order equation.
Such an equation might be made up as follows. ( To simplify calculation, the
time is unitary ).
With the necessary adjustments to their coefficients, a second order difference is equated to a first order difference and the n-th term, x,n, itself ( a zero order difference ). Such a second order difference equation is:
( x,n+1 + 2x,n - x,n-1 ) - 2( x,n - x,n-1 ) - x,n = 0.
This equation is essentially the Fibonacci difference equation, with the Fibonacci series as the x ordinate values, where x is a function of n, the number of terms reached. The equation reduces to:
x,n+1 - x,n - x,n-1 = 0.
If this were a second order differential equation, its coefficients ( here, 1, 1, and 1 ) would be adopted by an auxiliary equation, solved as a quadratic equation, just as the characteristic equation was solved ( above ). Here, the characteristic equation is the way to a short cut or algorithm for finding the n-th term, instead of successively working out a given series terms ( normally done by computer ) till reaching the n-th term.
Difference equations are finite approximations to differential equations, by turning a problem in calculus to a problem in algebra.
The transformation, T was found to be 1.618, the limiting ratio of y,n/x,n; or
- 0.618, the limiting ratio of y,n/-x,n. This was like solving the second
order equation ( of dependent variable, y,n, to independent variable, x,n ) as
y = 1.618x or - 0.618x. These are the linear equations of the eigenfunctions,
X and Y, ( whose eigenvalues are ) in terms of the original co-ordinates.
The second order differential equation, known as the damped wave equation, is a common-place in text-books. Engineering math books usually give worked examples, which is where Ive taken the following case of a force on a weight whose oscillations under-go slight damping, due to resistance from its immersion in a viscous fluid.
Without going into the details, the essential equation is:
d²y/dt² + 2.8dy/dt + 25y = 0.
The mid term is the resistance term, because resistance is assumed proportional to the velocity of the body. If this first order term were omitted, a simple undamped wave equation would be left. The coefficient of this first derivative is low compared to the coefficient of the y term, implying only slight damping of the oscillating body in question.
The dependent variable, y, is the displacement, at a given time, t, the
independent variable. This displacement might be of a weighted spring, made to
oscillate by a force pulling upon it. By Newton's laws the force is
proportional to the mass times acceleration. Acceleration is the second
derivative of displacement with respect to time ( the first term in the
equation ). And the force is equal and opposite to the displacement, which is
proportional to the elasticity of the spring.
Or, the factor involved might be the tension of a vibrating string, if the
displacement of a string is in question. ( The mass and elastic constants dont
show directly in the above equation, because they are combined into the
coefficient to the third term. )
As time goes on the oscillations, of the wave from crest to troff, will get smaller, as the wave dies away. The procedure for solving the value of y, is to consider the differential equation in terms of an auxiliary equation:
m² + 2.8m + 25 = 0.
The formula for solving quadratic equations ( quoted in an above section ) gives: m = - 1.4 ± 4.8i. For the case of slight damping ( when b² is less than 4ac in the quadratic formula ) the solution involves complex numbers.
This respective correspondence, of the the m terms to y and its first and
second derivatives, is to do with the special property of a solution of y that
can be put in terms of the exponent, a constant as important as pi. The
exponent, given the symbol e, or 'exp' for short, is an infinite number of
about 2.718...
This exponent is the sum of an infinite series of terms. The exponent to the
power of x, or exp(x) = xº/0! + x¹/1! + x²/2! + x³/3! + ...
The first term always equals one no matter the value of x. If x equals one, then the sum of the series is 2.718... ( to three decimal places ).
The derivative of each term equals the term before it, in the series. So, taking the derivative of the whole series, the exponential function, effectively leaves it unchanged -- no matter how many times one repeats the procedure, taking derivatives of derivatives. The exponential function remains unchanged under differentiations.
Generally, the derivatives of a function give a rate of change. Differential calculus measures growth. Exponential growth is the special case of a constant rate. Provided, say, y = A.exp(mt), where A and m are constants, the derivative of y leaves y essentially unchanged. The only difference that the first derivative brings is multiplication by m: dy/dt = Am.exp(mt). The second derivative repeats the process: d²y/dt² = Am².exp(mt). Where A and B are constants.
With luck, the problem of solving the second order equation ( in terms of y ) reduces to solving a quadratic equation ( in terms of m ).
Hence, in our example, y = A.exp(- 1.4+i4.8) + B.exp(- 1.4-i4.8).
For equations, mathematicians define as 'linear', the two solutions, in terms of m, can be added for a general solution.
Another way of expressing the solution for y is:
y = exp(-1.4t)(C cos 4.8t + D sin 4.8t). Where C and D are constants.
To solve numerically for y, the values of C and D may be found if the
initial conditions are known, such as of y at t = 0. In this text-book
example, y = - .4 at t = 0, so C = - .4.
In other words, at the start, t = 0, the diplacement is pushed from its
equilibrium position at y = 0, to - .4. Subsequently, the displacement bounces
back in the positive direction to its biggest oscillation, followed, in time,
by lessening oscillations, back and forth across the equilibrium line, till
coming to rest again.
This example, modified from a text book, also gave another initial condition, the velocity, at 16 feet per second, of the oscillating body, at t = 0, to ascertain the other constant, D.
The product rule of differentiation, for y with respect to t, is used on the right hand side of the equation for y, rendered as dy/dt, and set equal to sixteen. There turn out to be only two non-zero terms on the left hand side, under differentiation.
Hence, 16 = (-1.4 )( -.4 ) + 4.8D.
So, D is 3.22 ( to 2 dec. places ).
Actual values of the displacement, y, can now be found, at successive intervals of time, starting at t = 0, when y = - .4. For instance, after ( t = ) 0.29 seconds, the body has about reached its maximum amplitude of oscillation, or first and highest crest, at ( y = ) 2.06 feet ( to 2 dec. places ).
That is roughly the procedure of solving that kind of differential equation by differential calculus. Another means of solution is to turn the given differential equation into a difference equation, like that for the Fibonacci series ( shown in the previous section ) and solve it by the calculus of finite differences:
( a,n+1 - 2a,n + a,n-1 )/h² + ( 2.8(a,n - a,n-1))/h + 25a,n = 0.
Setting the intervals of time at h = 1/100 sec., this becomes:
10,000a,n+1 - 20,000a,n + 10,000a,n-1 + 280a,n - 280a,n-1 + 25a,n = 0.
This reduces to:
a,n+1 - 1.9695a,n + .972a,n-1 = 0.
In the same way, the formula for the nth term, in the Fibonacci series, was found. Applying the quadratic formula to the difference equation:
( -( -1.9695 ± ((-1.9695)² - 4(.972)) )/2
((-1.9695)² - 4(.972)) )/2
This equals .98475 ± .04762i.
The imaginary term prevents an addition and subtraction into two real numbers, which were then raised to the power of n, and added for the nth term formula for the Fibonacci series. But the imaginary number is an operator, implying a turn thru ninety degrees, so Pythagoras' theorem yields a hypotenuse, r = .9859.
( A hypotenuse, r, can be considered as the radius vector which sweeps out a circle. So, it remains of constant magnitude, while x and y co-ordinates, forming the other two sides of a right-angled triangle, are always changing. Repeated sweeps of the radius can be represented as a series of regular waves, in the more familiar graph of rectilinear co-ordinates.
Such an ordinary graph in which the wave crests and troffs are not uniform but decreasing, or 'damped', also has a corresponding picture, when considered as a circular function. The radius no longer sweeps out the same circle with each turn, but a decreasing circle, or a spiral. )
When r is raised to the power of n, it is equivalent to the exponential term, exp(mt), in the corresponding differential equation. That is, it also represents exponential growth or, in this case, decay.
That is: r'n ~ ( .9859 )'n ~ ( exp(-.0142.n) ~ exp(-1.4t).
Our finite difference equation was based on a calculation for every 1/100
of a second ( h = 1/100 ). We gave an example of calculating the differential
equation solution of y, when t = .29 or 29/100 of a second. In terms of the
finite difference equation, this means seeking a solution for its 29th term,
or n = 29.
Using the difference equation to solve for t = .29, n has to be divided by 100
( hn = t ). To compensate, its coefficient, -.0142, is multiplied by 100,
equaling -1.42, which approximates to, -1.4, the real number part of the
complex number ( and its conjugate number ) differential equation solution for
m.
Similarly for the trigonometric terms, involving the imaginary part, of the quadratic solution, .04762, multiplied by 100, as n is divided by 100, to become t.
Therefore, y = exp(-1.42t)( C cos 4.762t + D sin 4.762t ).
Using the same initial conditions, given for solving the constants C and D in the corresponding differential equation:
C = -.4 as before.
And 16 = (-1.42)(-.4) + 4.762D
So, D = 3.24.
For, t = .29, the difference equation solves for y = 2.058 ( to three dec. places ). This is the same ( to two dec. places ) as the more exact result from the differential equation. The difference equation's errors appear to have cancelled each other out. The correspondence between the two procedures isnt always quite so close.
Richard Lung.
References:
W W Sawyer: A Path To Modern Mathematics.
This commentary is a limited supplement and by no means a substitute for the
book.
An introduction to the meaning of calculus ( which I havent given here ) can be found in another book by W W Sawyer: Mathematician's Delight ( 1943 ).
A Geary, H V Lowry, H A Hayden: Advanced Mathematics For Technical Students. Part one.
For comments, criticism or corrections, please use the e-mail address on the home page.
To home page.