( Notation:
subscripts to a term are shown by a comma in between the term and the symbols
usually subscripted: x,n means the n-th term of x instead of the convention
that n is a sub-script.
Super-scripts, such as powers, are shown by a quotation mark between the term
and its power: x'n means x to the power of n. But the usual notation x² is
used for x squared. )
Links to sections:
We can use the technique of the characteristic equation for the much simpler wave equation, that is the undamped wave equation. If the damped wave equation, in its crude Fibonacci series version, were undamped, then the wave would maintain its original amplitude of ( plus or minus ) 0.618, at every subsequent crest and troff of its zig-zag cycle.
For simplicity's sake, make the maximum amplitude unity. A circle, of unit radius, can be crossed thru its centre by a vertical y-axis, of height, 1, and depth, - 1, and a horizontal x-axis, measuring 1 to the right, and - 1 to the left of circle centre. If you rolled out the circle circumference, it would measure two pi times the radius, as a horizontal ordinate in a Cartesian x-y co-ordinate system, instead of the circular or polar co-ordinates of radius, r, and angle ( say, angle Q ) swept out by the radius.
When x equals one or minus one, y equals zero, and vice versa. Take one complete anti-clockwise sweep of the radius, measured in terms of y = 1, at the top of the circle ( where x = 0 ) down to y = 0 ( where x = - 1 ) and down to y = - 1, at the bottom ( where x = 0 ) up to y = 0 again ( at x = 1 ) and right round to the top.
In terms of the equivalent Cartesian or rectilinear co-ordinates, a line
from y = 1, on the y-axis, would slant down thru the x-axis, at one quarter
of the length, 2(pi)r, reaching a troff at half that length, and
zig-zagging back up, in a similar manner. ( Each quarter point corresponds to
the radius sweep moving thru a quadrant of the circle, a 90 degrees angle. )
This would form a v-shape or simplest approximation to one wave-length, from
crest to crest.
For every complete sweep of the circle, another wave-length would follow on
along the x-axis in the rectilinear system, like a series of ripples in a
pond.
The algebra of these repeated sweeps or repeated wave-lengths is a periodic series: 0, -1, 0, 1, 0, - 1, 0, 1, 0, - 1, 0, 1,..
In the anti-clockwise sweep of the circle, divided into quadrants by x-y axes, x measured this series, from the first term, whereas the y-ordinate paired off, from the second term in the series, with the x-ordinate. This was also the case with the previous web-page treatment of the Fibonacci series, which we now repeat, using the characteristic equation.
We take for the first two x-y pairs ( the initial conditions ) of this circular series, x = 0 and y = 1, x = - 1 and y = 0. These are a, b, c, d, respectively, in the characteristic equation:
T² + ( a + d )T + ( ad - bc )I = 0.
Therefore, T² + 1 = 0. And T = +i or -i. ( Where i equals the square root of minus one. )
( Notice that the mid-term, the first order term in T is missing. Considered as an auxiliary equation to a wave equation, this missing term dissipates the energy of the wave. This indicates a simple wave equation without a damping effect on the amplitude. )
Plus or minus i are the eigenvalues of two new axes, X and Y, which eigenfunctions undergo no expansion or contraction, because both values are unitary. The equation of Y is: iy = - x. The equation of X is: iy = x. Therefore, the new axes appear at 45 degrees to the old, so the circle is split into eight equal segments.
As for finding the n-th term of the Fibonacci series, the eigenvalues can be used to find the n-th term of the periodic series, x,n:
x,n = C( i )'n + D( - i )'n.
Taking x,n = 0, C + D = 0. Therefore, C = - D.
Taking x,n = - 1,
- 1 = iC - iD. Therefore, - 1 = 2iC. Or, C = i/2. And D = - i/2.
Substituting:
x,n = ( i/2 )( i )'n - ( i/2 )( - i )'n.
Table three shows how this formula works for the first five terms. Tho,
simple arithmetic for this four-term periodic series, more easily guides us
to the answer, rather as we know which year is a leap year:
Let n be any odd number. All the terms, whose order in the series is odd,
equal zero: x,n = 0.
Let n+1 be all the even ordered terms. All these terms, from the second term
onwards, whose number order is divisible by two but not by four, equal minus
one: x,(n+1)/2 = - 1.
All these terms, from the fourth term onwards, whose number order is
divisible by four, equal plus one: x,(n+1)/4 = 1. Therefore, x,n = x,(n+1)/2
+ x,(n+1)/4.
| n | ( i/2 )( i )'n | - | ( i/2 )( - i )'n | x,n |
| 0 | i/2 | - | i/2 | 0 |
| 1 | - 1/2 | - | 1/2 | - 1 |
| 2 | - i/2 | - | - i/2 | 0 |
| 3 | 1/2 | - | - 1/2 | 1 |
| 4 | i/2 | - | i/2 | 0 |
Knowing the n-th term of x, x,n, also determines its y partner, which
equals the followng term in the periodic series: y,n = x,n+1. Taking x and y
together as a complex variable, we also know the n-th complex number, z,n =
x,n + iy,n.
Complex numbers refer to ordered pairs of numbers, that can locate or
co-ordinate any point on a plane.
We noted that the new X-Y co-ordinates split the circle into eight
segments. There is no reason why we should not use them to plot an eight term
periodic series, instead of four. The amplitude, at the four new points, at
forty five degrees to where the original x-y co-ordinates touched the
circumference ( derived from the sine of that angle, given a radius of one
for the hypotenuse ) is about 0.707.
The new periodic series would be: 0, - .707, - 1, -.707, 0, .707,
1,..repeated.
Translating this more detailed series, from circular or polar co-ordinates to rectilinear co-ordinates, the v-shaped wave would undergo a second approximaton, to the normal smooth curve, with bends near either side of the crest and troff of the wave-length, giving a first indication that a wave curve has shallower slopes there.
Further sub-divisions of the circle would translate into closer approximations to a smooth wave shape. In this way, a difference equation approaches a differential equation, the ordinary wave equation.
All the mathematics jargon, of this section title, expresses some quite simple ideas. The real and imaginary parts are simply the ordered pairs of numbers, labelled x and y, respectively, from the previous section. The y ordinate is multiplied by the letter i ( for imaginary ). Then the x and y ordinates are paired with an addition sign and called a complex number, denoted z, like so: z = x +iy.
This can be represented on a graph of x and y, where y is the vertical and x is the horizontal axis. But this is not to be confused with the traditional graph of y as a function of x, expressing a ratio of y over x, or y/x, like velocity equals distance traveled over time.
The complex number serves a dfferent function, namely to pin-point every possible spot on a plane or square, marked-off by the x and y axes. In particular, z may represent every possible point on the circumference of a circle, whose centre is drawn from the origin of the x and y co-ordinates. ( See graph of the complex number. )
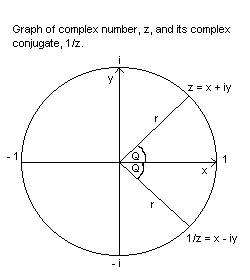
On the graph, the x and y quadrants are marked 1, i, - 1, - i. This is actually a short-hand for the four positions of the complex number z, where either x or y is zero. The full description of z at these four points is, respectively: z = x + iy = 1 + i0, 0 + i1, - 1 + i0, 0 - i1.
The graph shows a particular point for z on the circle rim, indicated by a radial line, r ( for radius ) at an angle of Q degrees between the x-axis and the radial line. ( The usual symbol for the angle is not Q but Greek letter theta. )
The graph also shows a mirror image or reflection of point z, below the x-axis. It so happens, that when one works out the algebra, this mirror image position comes to the inverse of z, or 1/z, which equals x - iy. This mirror position has a special name, called the complex conjugate. ( It also has a special symbolisation of the letter z given a tilde, or wavy line, over it. We'll have to use "Z" here. ) Generally, the complex conjugate equals r²/z. But here we take r = 1.
The complex number z and its complex conjugate, 1/z, are vectors, radius vectors, in this case. That is, they have both magnitude, in the length of the radius, r, and they have direction, in the angle Q of the radius with the x-axis. The vector z is changed or transformed, by mirror reflection, into its conjugate vector, 1/z. But in that process, the co-ordinates x and y are not changed in direction. Considered as vectors in their own right, they are so-called eigenvectors, or vectors that dont change their direction under a transformation, such as mirror reflection.
This is as it should be, because the problem of finding eigenvectors, is the task of finding the co-ordinates that state a mathematical situation most transparently, for the solving of problems.
However, eigenvectors have eigenvalues. This simply means that their magnitude may be changed: they may stretch or shrink. In the example of the graph, the x-axis remains unchanged by mirror reflection. In effect, it is multiplied by one, or its eigenvalue is plus one. The effect of mirror reflection on the y-axis is to multiply it by minus one, for an eigenvalue, because the complex conjugate is on the negative y-axis.
The fore-going explanation of x and y as eigenvectors can be presented, loosely, in terms of a theorem that every function can be split into a symmetric function and an anti-symmetric function. These are eigenvectors, because a symmetric function is one which is left unchanged by an operation upon it, just as the x-axis was left unchanged by mirror reflection of z into 1/z. Also, an anti-symmetric function merely changes the sign of a function, as the sign of the y-axis changed, thru mirror reflection of z into its complex conjugate, 1/z.
( Symmetry derived from geometrical considerations. For instance, the human face is roughly symmetrical. If the hair is parted down the middle of the head, then the mirror image's parting will be, too. The mirror image leaves the head's middle parting unchanged: their partings are symmetrical. But a left-parted head of hair will have a right-parting for a mirror image. A parting on one side and its reflected image are anti-symmetrical to each other. )
The theorem of symmetric and anti-symmetric parts is stated in terms of the standard text-book formulas ( given here without proof ) for z and Z (usually z with tilde on top) in terms of rectilinear co-ordinates x and y, and polar co-ordinates, r and Q ( here standing in for angle theta ):
z = x + iy = r ( cos Q + i sin Q ) = r exp(iQ).
Z = x - iy = r ( cos Q - i sin Q ) = r exp(-iQ).
Adding the two sets of equations:
z + Z = 2x.
This can be shown to be a symmetric expression under the operation of mirror reflection, denoted M. This operator works similarly to the operator, i, which applied to y means a turn thru ninety degrees with respect to the x-axis. The difference is that M reflects z, thru the angle Q about the x-axis, from the positive y-axis onto the negative y-axis. Another operator used is the Identity operator, I, when applied to a function, merely leaves it as it is: Iz = z = 1z. So, I = 1. ( This was used, on the previous web page, in the characteristic equation. )
Hence, Mz = Z.
So, 2x = z ( 1 + M ) = z(I + M).
But a mirror operation applied twice ( denoted by M² ) produces a situation identical to the original:
M² = I or M² - I = 0.
It follows that: z ( M² - I ) = 0 = z ( M + I )( M - I ) = 2x ( M - I ).
Therefore, Mx = Ix. In other words, the operation of reflection on x is the same as the Identity operation on x. Or mirror reflection produces no change on x.
One can also subtract Z from z, for 2iy. Following the same reasoning, as for x, this shows My = - Iy, or that the mirror operation on y changes its sign, so that it is anti-symmetric with the identity of y.
For example, the wave equation could describe the regular oscillations, over time, of a spring, of elasticity, k, with a bob, of mass, m, on the end. The mass pulls the spring down and the elasticity pulls it back in a continuing jig. A simplified form of the equation has k and m equal, or k/m = 1. Normally, k/m is set equal to w², the square of the angular frequency, which appears in the equation as the coefficient of the dependent variable.
The frequency, f, is the number of oscillations per unit time; w = 2πf. ( This is a relation w and f share for the case of circular motion, when w is called the angular velocity. )
The equation arises from Newton's law that force is proportional to accelerating mass: F = ma. The force, F, is in equal and opposite reaction to the elastic constant, k, with regard to a displacement distance of oscillation, x, so that F = - kx. The acceleration is a second order change of distance with time, involving a second derivative ( d²x/dt² ).
The up and down of the displacement, x, about a spring's equilibrium position, can be mimicked by the changing amplitude of a radius sweep around a circle, like a clock face that keeps time with it. Alternatively, in rectilinear co-ordinates, the changing amplitude of the displacement x, measured on the vertical axis, undergoes a wave motion over time, measured on the horizontal axis.
Call the radius-sweep angle, Q. This equals angular frequency, w, times time, t. The sine of Q equals displacement, x. Or, x = sin Q = sin wt.
The acceleration, a, ( which is the second derivative of the distance, x, with respect to time ) is: d²x/dt² = - w² sin wt = - w²x.
( We have left out a couple of things. Sin wt is a multiple of
the maximum amplitude, A, the height of the wave crest, or depth of the
troff, from equilibrium level, which for water is the surface level. We
assumed, at the start that A = 1.
Also, a phase angle, a, is generally included so x = sin ( wt + a ).
Making angle, a, equal ninety degrees would be to start at the top of the
vertical axis, ninety degrees on from the positive horizontal axis. This is
equivalent to x = cos wt. And, in fact, this is where we did start
the simple periodic series, described above. )
Hence, F = ma = - w²xm = - kx.
So, md²x/dt² + kx = 0. Or, d²x/dt² + w²x(t) = 0.
Under previous simplifications, w² = k/m = 1.
So, d²x/dt² + x = 0. This ordinary wave equation for the oscillating spring, or analgous physical motions, describes the above periodic series, as the intervals between the terms close so much, that the function becomes, in effect, continuous.
Richard Lung.
(Minor corrections 28 feb. 2007).
References:
W W Sawyer: A Path To Modern Mathematics.
G Stephenson: Mathematical Methods For Science Students. ( 1973 )
For comments, criticism or corrections, please see e-mail address on home page.
To home page.